ML95
Lt. Junior Grade
- Registriert
- Aug. 2012
- Beiträge
- 366
Hallo zusammen,
derzeit bearbeite ich eine Aufgabe zur Aussagenlogik, genauer gesagt zur Implikation. Dabei stellte sich mir eine Frage bzgl. der Klammersetzung.
Ich möchte natürlich keine Musterlösung von euch und habe auch eine Vorahnung bzgl. der Frage auf deren Grundlage ich die Aufgabe schon fertig bearbeitet habe. Es geht mir also lediglich um eine Bestätigung oder Widerlegung meiner Vorahnung
Konkret geht es um die Frage, ob man folgendes annehmen kann:
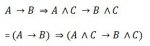
Meiner Meinung nach kann man das doch so schreiben, oder? Es soll nach meinem Verständnis doch durch die erste Zeile ausgedrückt werden, dass wenn die Implikation A-->B gilt, allgemeingültig gilt A^C --> B^C. Das würde ja durch die Klammern in der zweiten Zeile ausgedrückt werden.
Über eine kurze Rückmeldung würde ich mich sehr freuen.
Danke sehr
derzeit bearbeite ich eine Aufgabe zur Aussagenlogik, genauer gesagt zur Implikation. Dabei stellte sich mir eine Frage bzgl. der Klammersetzung.
Ich möchte natürlich keine Musterlösung von euch und habe auch eine Vorahnung bzgl. der Frage auf deren Grundlage ich die Aufgabe schon fertig bearbeitet habe. Es geht mir also lediglich um eine Bestätigung oder Widerlegung meiner Vorahnung
Konkret geht es um die Frage, ob man folgendes annehmen kann:
Meiner Meinung nach kann man das doch so schreiben, oder? Es soll nach meinem Verständnis doch durch die erste Zeile ausgedrückt werden, dass wenn die Implikation A-->B gilt, allgemeingültig gilt A^C --> B^C. Das würde ja durch die Klammern in der zweiten Zeile ausgedrückt werden.
Über eine kurze Rückmeldung würde ich mich sehr freuen.
Danke sehr