[Mathe] Berechnung von der Schnittmenge 2er Kreise

[Executor55]

Hallo ich stehe hier vor einem Matheproblem:

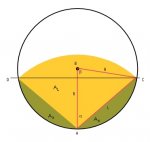
[B]Aufgabe[/B]
Gegeben:
Kreis k1 mit Radius r1, Fläche a1 und Mittelpunkt m1
Kreis k2 mit Radius r2, Fläche a2 und Mittelpunkt m2
m2 liegt auf k1 -> Abstand m1 zu m2 = r1
Schnittmenge von a1 und a2 = hälfte von a1

Gesucht:
Radius r2 in Abhängigkeit von r1

Hi
ich weis nicht ob ich hier im richtigen Forum geschrieben habe (ggfs. bitte verschieben).
Ich habe eine Frage die ich aus keinem Mathebuch habe sondern die mir jemand als Knobelaufgabe gestellt hat.
Ich komme aber nicht drauf und bräuchte da mal hilfe.

Ich bin schon zu lange aus der Schule um das alles Mathematisch korrekt zu formulieren. Tut mir leid.
Ich hoffe aber die Aufgabenstellung ist verständlich rübergekommen.
Ich möchte natürlich auch die Herleitung des Ergebnisses (falls es jemand beantworten kann) sehen und verstehen.

Danke für Antworten.

 

[ag3nt]

Was meinst du mit "m2 liegt auf k1" ?

1. Der Abstand zwischen m1 und m2 < r1
2. Der Abstand zwischen m1 und m2 = r1
3. k2 beschreibt eine echte Teilmenge von k1

 

[kühle BOckwust]

hm,also sicher das du dir die aufgabe nicht doch nochmal anschauen willst?denn so schwer ist sie nicht....schau dir doch einfach nochmal die sache mit der schnittmenge ab.evt kannst du dir ja eine gleichung aufstellen die sich über die flächen defniert.

falls der tip nicht geholfen hat kann ich aber gerne die lösung posten.

ansonsten viel spass beim knobbeln.

gruss
flo

 

[peda2411]

Klingt ziemlich interessant ....

*grübel grübel*

P.S.: @kühle BOckwust: du kannst es ja als Spoiler posten, dann muss es derjenige, der es nicht wissen will auch nicht lesen.

 

[1668mib]

@ag3nt: Ein Kreis ist der geometrische Ort aller Punkte, die von einem Punkt den selben Abstannd (Radius) haben, es ist also eindeutig dass die Entfernung von M1 und M2 = r1 ist. (sonst würde es ja heißen "liegt in a2" und dann könnte man ja auch kaum sinnvoll Abhängigkeiten ausdrücken)

btt: Ich vermute dass du mit Hilfe der Kreissegmente auf die Lösung kommen kannst
Fläche eines Kreissegments findet man z.B. hier: http://de.wikipedia.org/wiki/Kreissegment
(die winkellose Formel mit r, h und s wohl)
kann mich aber auch irren :-)

Edit: Da hab ich ja wohl Blödsinn geschrieben ich hab eine zu leichte Formel angenommen :-)

 

[ag3nt]

@1668mib

Da Executor55 selbst gesagt hat, dass er sich nicht sicher ist ob er es korrekt beschrieben hat, habe ich lieber nachgefragt! Umgangssprache ist nun mal selten präzise, was gesagt wird ist noch lange nicht was gemeint ist.
BTW: deine Definition ist unvollständig (eine Kugel könnte man z.B. genauso beschreiben) aber ich will hier ja nicht den Oberlehrer spielen.

 

[1668mib]

Da hast du natürlcih recht... aber wir betrachten das ganze ja eh nur 2 dimensional...
Aber wenn jemand sagt "liegt auf dem Kreis" ist das sehr eindeutig, wie gesagt: Anders könnte man gar nichts vernünftiges sagen.

 

[Executor55]

Also natürlich meine ich: Abstand von m1 zu m2 = r1 (oben ausgebessert)
Kleines Bild zum besseren Verständnis:


Mein erster Lösungsansatz war ja auch das mit den Segmenten.
So das ich das Segment 1 ausrechne -> Segment vom Kreis k1, das von der Strecke AB getrennt wird.
Das dann mit dem Segment 2 addiere -> Segment vom Kreis k2, das von der Strecke AB getrennt wird.
Und das Ergebnis dann halt von der Fläche a1 abhängig mache bzw. mit der Hälfte von a1 gleichsetze.
Und der Satz des Pythagoras spielt keine unwesentliche Rolle in dem Dreieck da um die Formel für die Segmente zu vervollständigen. (glaube ich)

Also ich denke mal der Ansatz wird schon richtig sein aber die Umsetzung mit den ganzen Formeln und der auflösung nach r1 wird halt dann das Problem

Ich werde is das Wochenende mal versuchen und schauen wie weit ich komme.
Aber erstmal danke für Antworten, hätte nicht gedacht wie viele Mathe Interessenten das CB Forum liefert.

 

[Gentlem4n]

(x − xM)² + (y − yM)² = r2
Ich würd dann die beiden Kreisgleichungen gleichsetzen und nach r2 auflösen? Oder denk ich da zu einfach?

 

[ag3nt]

Nein, das geht nicht.

Ich bezweifle auch stark, dass das Problem mit Schulmathematik lösbar ist, ich selbst kenne nur eine Numerische Lösung für das Problem, aber die Formel würde mich auf jeden Fall interessieren, wenn es sie gibt.

edit:
Da jetzt schon mehrere glauben, dass das Problem so einfach zu lösen sei, gebe ich einfach mal den Tipp die Gleichung nach r1 bzw r2 umzustellen. Ziel ist es immerhin die Größe von r2 im Verhältnis von r1 anzugeben. Wer es schaft diese Gleichung ohne(!) Numerik zu lösen der poste mal bitte den Beweis dazu, dass es geht - Die Gleichung aufzustellen ist nämlich absolut nicht das Problem!

btw: Das Rätsel ist auch als "die grasende Ziege" bzw unter ähnlichen Namen bekannt.

 

[allli84]

1668mib hat recht, mit der Wiki Seite ist es relativ einfach lösbar.
Fläche k1= Fläche der 2 Kreissegmente
Für die Fläche der Kreissegmente ist r einfach ablesbar jeweils. Über den Sinussatz stellt man das Verhältnis zwischen den beiden Segmenten her. Ein Segment kann man mit den gegebenen Formeln ausrechnen, damit auch das andere. Kreisgleichung eliminiert dann alles bis auf r1 und r2.

 

[Executor55]

Aber der Sinussatz bringt doch eine neue Variable mit sich, wenn nicht sogar 2. Den Winkel Alpha (Am1B) und Beta (Am2B). Und einen Zusammenhang der Winkel kann ich nicht erkennen, da Gamma (m1Bm2) unbekannt ist.
Sorry aber ich komm nicht drauf.

 

[Executor55]

Also ich komm einfach nicht drauf.
@ allli84 oder kühle BOckwurst
Hätte gerne die Lösung von euch mit Herleitung
Danke

 

[peda2411]

Würde jetzt auch endlich gerne wissen wie das geht...

@Executor55

Doppelposts sind hier nicht gerne gesehen. (ÄNDERN - Button benutzen!)

mfg

 

[ag3nt]

@ allli84 oder kühle BOckwurst

Ich wäre jetzt auch mal an einer Lösung von euch interessiert, sonst werde ich das mal demnächst auflösen (sobald ich die Zeit dazu finde, ist nämlich nicht so trivial zu erklären).

 

[Executor55]

Also ich hab das jetzt letzt nochmal alles probiert und ich komm und komm einfach net weiter.
Und diese Wikipedia Seite bringt mich auch null weiter, weil da überall noch ne weitere unbekannte dazukommt, nämlich der Winkel Alpha, den ich ja auch nicht hab oder berechnen kann.

Kann das mal bitte jemand lösen ... danke

 

[ag3nt]

Also erstmal muss man natürlich die Basisgleichungaufstellen, in dem Fall ist das eine Schnittmenge von 2 Kreisen, die Gleichung dafür sieht so aus:

Seien:

• R := Der Radius des Kreises 1
• r := Der Radius des Kreises 2 (Länge der Leine)
• d := Der Abstand zwischen den Kreisen

Da d = R, lässt sich schon mal einiges vereinfachen

Da wir nur die relative Größe von r zu R suchen, lässt sich vereinfachend annehmen, dass R = 1 gilt:

Da die gesuchte Fläche der Hälfte des Kreises 1 entspricht lässt sich damit die Gleichung vervollständigen:

Damit wäre die Gleichung vollständig, aber da der arccos eine transzendete Funktion ist, kann man an dieser Stelle nicht mehr weiter machen, sondern muss die Gleichung numerisch lösen.
Da allli84 und kühleBOckwurst ja der Meinung waren, dass die Gleichung so einfach zu lösen ist, bin ich an dieser Stelle wirklich mal gespannt wie ihr beiden das gemacht habt (falls möglich würde mich diese Lösung wirklich brennend interessieren).

 

[Photon]

ag3nt: Womit hast du die Formelgrafiken gemacht?

 

[ag3nt]

Hiermit http://thornahawk.unitedti.org/equationeditor/equationeditor.php

 

[Executor55]

Erstmal rießen Dank an dich ag3nt für die Mühe.
Halbwegs diesen Lösungsansatz hatte ich ja auch schon ... du hast mit deiner vereinfachten Annahme von "R = 1" noch einen Schritt mehr gemacht als ich, auf den ich nicht gekommen wäre, den ich aber sehr gut finde.
Hierbei müsste man ja bloß durch Annäherung (...heißt das glaube ich ^^) versuchen auf 0 = 0 zu kommen um den Wert von r zu ermitteln, richtig? Dieser dürfte dann schätzungsweise zwischen 1.1 und 1.3 liegen (ungefähr )
Ohne meinen exponentiellen Taschenrechner aus der schule kann ich das leider nicht genau ausrechnen.

Da allli84 und kühleBOckwurst die ganze Zeit von einer sehr einfachen Lösung sprachen, dachte ich, das ich hiermit auf dem falschen Weg wäre und mir irgendwas entgehen würde.
Wie sich jetzt allerding herausstellt, war ich garnich mal so falsch.

Ich hoffe doch sehr, das wenigstens einer der beiden nochmal Antwortet.

PS:
ach ja wie du die 4 Klammern in der letzten Wurzel gekürzt hast erklärst du mir dann mal ein anderes mal

//EDIT: hat sich schon erledigt ... habs selbst rausgefunden ... ich blinder ^^