[Matlab] Matrix mit negativen Werten spuckt NaN/Inf aus

[Müs Lee]

Ahoi.

!!!Vorab!!! Ich weiß, dass CB kein Hausaufgabenboard ist. Ich will auch keine fertige Lösung, nur Denkanstöße und eventuell sieht jemand ein paar Fehler.

Unser Prof hat im Fach Modellbildung/Simulation jedem Studenten eine Testataufgabe aufertragen. Meine lautet wie folgt:

An sich keine so große Sache, nach ein wenig Einarbeiten gelingt es größtenteils. Hier der Code:


a=0;
e=10;
i=a;
j=i;
n=10;


x=linspace(a,e,n);
y=x;
[x,y]=meshgrid(x,y);
z=(2*x.*y.^2)/(x.^2 + y.^4);

for j=a:e,
for i=a:e,
if x<0
z=0;
elseif x==0
z=0;
end
end
end


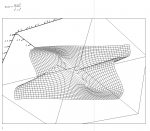
mesh(x,y,z)


z sieht damit so aus:

Wenn a allerdings ein negativer Wert ist, zB a=-10 und e=10, erhalte ich die Fehlermeldung Warning: Matrix is singular to working precision.

z ist somit

und det(z)= NaN

Wenn a=-10 und e=-1 kommt

??? Error using ==> mesh at 80
Z must be a matrix, not a scalar or vector.

Keine Ahnung, was ich damit anfangen soll. z ist doch immer noch eine Matrix?

Wenn a=-10 und e=0 kommt lediglich Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.001188e-020. Diese Meldung kommt eigentlich immer, aber damit erhalte ich immerhin ein Resultat.



Ich kann nicht nachvollziehen, warum ich solche riesigen Zahlen mit 1.0e+017, NaN und +-Inf rauskriege, obwohl die Funktion ja keine sonderlich hohen Potenzen beinhaltet und die Parameter sich dermaßen ändern. Irgendwie muss es doch möglich sein, einen negativen Zahlenbereich einzuschließen, da sonst die Hälfte der Aufgabe hinfällig ist. Laut WolframAlpha kann man die Funktion nicht anders ausdrücken, das hätte vielleicht geholfen. Der Plot von WA bewegt sich in xyz auch nur im Bereich von +-1, bei meinem geht die Skala ja bis 10^17...

Schon mal Danke im Voraus für jeglichen Input, im Moment komme ich überhaupt nicht weiter.

 

[stupidus]

Hast du überprüft, ob x und y auch richtig erzeugt werden? Bzw. das was beim Befehl meshgrid rauskommt richtig ist.

 

[Müs Lee]

Ja, die werden korrekt erstellt.

 

[InteGralFormat]

Hi.

Also ich hab keinerlei Ahnung von Matlab und dessen Syntax. Vom Prinzip her find ich aber die Aufgabenstellung interessant.

Ich nehme an, du willst den Graphen von f im R³ darstellen.
Dabei sollen die Achsen im Intervall [a,e] dargestellt werden. Es sollen in jede Richtung Funktionswerte berechnet werden und diese in einer Matrix gespeichert werden.

Sind meine Annahmen erstmal korrekt?

Dann erzeugst du einen Vektor x, der n Werte zwischen a und e beinhaltet.
Den Vektor y setzt du identlisch x.
Danach lässt du dir eine Tabelle erzeugen, die aus den Vektoren x und y gebildet wird.
Schlusslich ist die Definition von z als Funktion von x und y.

Da die Formel für z nicht in der Schleife zur elementweisen Berechnung der z-Matrix-Elemente in der Schleife steht, nehm ich an, dass Matlab automatisch die Dimension von z erkennt und dementsprechend berechnet?


Was mir jetzt nicht in den Kopf will: Die Schleifen.
Du hast eine doppelte Schleife, die augenscheinlich für alle Elemente der z-Matrix überprüfen soll, ob die Bedingung x<0 für das Matrixelement (j,i) erfüllt ist und dementsprechend Nullen soll. Dafür verwendest du die Zählvariablen i und j im Bereich von a .. e.

Eigentlich bräuchtest du ja erstmal nur die Werte prüfen bzw. aktualisieren, für die ein Element aus x den Wert 0 hat. Wenn x = (1 2 3 4 5 6 7 8 9) brauch ja gar keine Überprüfung stattfinden. Wenn x = (0 1 2 3 4 5 6 7 8 9) brauch nur eine Aktualisierung der Werte für z Spalte z (1, i) stattfinden, sprich ein Schleife reicht aus.

Weiterhin: x ist ein Vektor, wie du ihn ja definiert hast. Die Abfrage ob x < 0 ist macht doch nur Sinn, wenn man ein Vektorelement aus x mit 0 vergleicht, oder? Ich vermisse irgendwie die Form "if x(i,j) < 0" ... sprich mir fehlt der allgemeine Bezug zu den Zählvariablen i und j.

Im Endeffekt wird jetzt i*j fach die gleiche Abfrage gestartet, die jedes mal das selbe Ergebnis bringt, oder?


Zumindest ist es so, wie ich es aus Programmiersprachen her kenne.

Eine Frage: Was macht Mathlab bei Division durch 0? Für x=y=0 erkennt Matlab das, oder nicht?
Noch eine Frage: Kann Matlab bei For-Schleifen von von negativ nach positiv bzw. von positiv nach negativ zählen?

Die zweite Fehlermeldung könnte ich mir dadurch erklären, dass die Matrix im Endeffekt ja nur einen Vektor darstellt - jede Zeile ist der Vektor. Die Determinante sollte immer Null sein, wenn die Matrix aus Zeilen bzw. Spaltenvektoren besteht, die nur eine Linearkombination voneinander sind. Weiterhin: Die Determinante ist nur für quadratische Matrizen definiert.


Wenn ich das Problem jetzt irgendwie in einer normalen Programmiersprache lösen sollte, würde der Code bei mir so aussehen:

a=0;
e=10;
n=10;

x=linspace(a,e,n);
y=x;
[x,y]=meshgrid(x,y);

for j=a:e, # geht alle Spalten durch (der x-Vektor beschreibt die Spalten)
if x[j]=<0, # fall der korrespondierende x-Wert kleinergleich 0 ist, setzt die j-te Spalte gleich Null.
for i=a:e,
z[i,j]=0;
end
elseif # sonst, berechne für jede Zeile die z-Werte
for i=a:e,
z[i,j]=(2*x[j]*y^2)/(x[j]^2 + y^4)
end
end
end

Da würde durch die Schleife jeder Wert für die z-Matrix berechnet. Jede Spalte, für den ein Element von x gleich Null ist, bekommt ebenfalls den Wert Null.


Wiegesagt - keine Ahnung von Matlab, nur eine generell Idee von Mathe und ein wenig Programmierung

 

[stupidus]

Bezüglich folgenden Codes dachte ich auch erst, dass das falsch sein muss, aber dann dachte ich mir, vielleicht ist es ja irgendeine obskure Matlabfunktion. Nachdem ich es ausprobiert habe, bin ich mir aber sicher das das falsch ist.

for j=a:e,
for i=a:e,
if x<0
z=0;
elseif x==0
z=0;
end
end
end


Die richtige Variante wäre es, die Elemente von x über ihren Index durchzugehen. D.h. du lässt ersteinmal i von 1 bis n laufen. Danach musst du dann x(:,i) oder x(i,: ) abfragen und z(:,i) entsprechend setzen. (Welche Variante richtig ist, musst du selber überlegen).

Trotzdem stimmt irgendwo anders noch etwas in dem Code nicht, da für positive x und y nie etwas negatives rauskommen dürfte.

 

[Müs Lee]

@ InteGralFormat: Aufgabenstellung korrekt erkannt.

Die Dimensionen von z werden durch meshgrid festgelegt (ein 2D-Netz in der xy-Ebene wird erstellt), durch z=... bekommt jede xy-Koordinate einen z-Wert. Der Einfachheit halber habe ich eine quadratische Matrix gewählt.

Ja, die Schleifen sind so eine Sache. Das Programm ist noch eine Baustelle und die Schleifen waren eher zweckmäßig, um erst mal die Erfüllung der Bedingung f=0 für x<=0 für alle Werte sicherstellen zu können. Prinzipiell hast du aber recht und deine Lösung ist eleganter. Es liegen halt zwei Semester zwischen dieser Aufgabe und dem letzten Mal Programmieren, ich bin leider nicht mehr so fit darin bzw. war es nie . Ich bin Maschinenbauer in spe und habe nur rudimentäre C++ und Matlabkenntnisse.

Matlab kann in beide Richtungen zählen. Bei 1/0 kommt Inf raus, bei 0/0 NaN. Aber gut, dass du das ansprichst. Ich erhalte also mit Sicherheit Werte zwischen +-eps und damit 0/0 sowie Zahl/0. Interessanterweise zeigt mir Matlab ein eps von +-2.2204*10^(-16), es sollte laut Google aber 2^(-52) sein, da es standardmäßig mit double arbeiten sollte... Dass dann solche Werte rauskommen ist kein Wunder.


Bliebe die Frage, was ich mit diesen Werten anstellen soll. Entweder umschiffe ich das, indem die x-Werte einfach nur von x>=0 starten (was ja im Endeffekt das Gleiche wie die Schleife erledigen würde) oder ich begrenze die Werte nach oben und unten, was eine Kastration sondergleichen darstellen würde...


@ stupidus: Du hast recht. Als ich das so geschrieben hatte, hatte ich irgendwie im Kopf dass dies für alle xy-Paare geschehen müsste, wo doch ein Durchlaufen von x ausreicht. Bzw. keine Ahnung was ich da gedacht habe. Ich bastele später noch ein wenig dran rum, aber gerade sehe ich den großen Unterschied nicht. Bei der falschen Vorgehensweise durchläuft das Programm die Schleifen doch nur unnötig oft und ändern an sich nichts am Ergebnis, oder stehe ich gerade auf dem Schlauch?

 

[stupidus]

Deine Berechnung von z stimmt nicht, du musst alle Operationen elementweise ausführen. Du hast da eine vergessen

Bezüglich der Schleifen beachte einfach das was ich oben geschrieben habe. Bei mir funktioniert es auf die Art jetzt richtig.

 

[Müs Lee]

Das elementweise Ausführen wird doch durch die Punkte hinter den Variablen in z= x.blabla ausgeführt, oder nicht? Zumindest habe ich das so mehrfach im Internet gefunden. Oder was meinst du mit "alle Operationen"? Mehr sind ja eigentlich nicht drin, oder meinst du die Schleife?

 

[stupidus]

Ich meinte, dass die Zeile z=(2*x.*y.^2)/(x.^2 + y.^4); falsch ist. Da fehlt noch ein Punkt. Die richtige Stelle zu finden überlasse ich dir.

Dein Schleifencode ergibt so wie er da steht überhaupt keinen Sinn. Du musst über die Elemente von x iterieren. Und diese Elemente mit Indices ansprechen. Und so ein Index kann nun mal nicht negativ sein. D.h. du musst i von 0 bis n laufen lassen. Mit x(:,i) sprichst du dann die i-te Zeile (oder Spalte, bin mir da nie sicher) an.

EDIT: Die Punkte gehören übrigens nicht hinter die Variablen, sondern vor die Operationen. Kleiner, aber feiner Unterschied.

 

[Müs Lee]

Ah, gut zu wissen! Danke fürs Input, ich setze mich dann bald noch mal dran.

Ergo so?

a=-100;
e=100;
i=a;
j=i;
n=10;


x=linspace(a,e,n);
y=x;
[x,y]=meshgrid(x,y);
z=(2*x.*y^2)./(x^2 + y^4);

mesh(x,y,z)


Scheint sehr viel besser zu sein, keine Fehlermeldung und der Plot sieht auch ganz anders aus.

 

[stupidus]

Du hast zwar die richtige Stelle für den Punkt gefunden. Aber warum hast du ihn an anderen Stellen wieder entfernt?

 

[Müs Lee]

Nicht nachgedacht. So sieht das Ganze schon sehr nach der Lösung von WolframAlpha aus.

a=-100;
e=100;
n=10;


x=linspace(a,e,n);
y=x;
[x,y]=meshgrid(x,y);
z=(2*x.*y.^2)./(x.^2 + y.^4);

mesh(x,y,z)

Um die Schleife kümmere ich mich dann baldigst. Zuvor muss aber eine Runde Schlaf sein . Vielen Dank für die Hilfe!

 

[InteGralFormat]

Die richtige Variante wäre es, die Elemente von x über ihren Index durchzugehen. D.h. du lässt ersteinmal i von 1 bis n laufen. Danach musst du dann x(:,i) oder x(i,: ) abfragen und z(:,i) entsprechend setzen.

Das hatte ich glatt übersehen. Die Frage muss man aber differenziert betrachten. Wie ist die Matrix bzw. ein Vektor in MatLab definiert? Sollte die Matrix so definiert sein, dass das erste Element (also Schnittstelle erste Zeile. erste Spalte) als a;a definiert ist, dann würde es passen. Halt ich aber für höchst unwahrscheinlich, dass es so wäre.
Daher müsste man also die Zählvariablen von 1 bis (a-e) laufen lassen, damit die korrekten Elemente angesprochen werden. Würde hier eine Schleife von 1 bis 10 ergeben, also 10 Elemente.

Die Alternative wäre der Code hier:

K=0;
L=0;

for j=a:e step (a-e-1)/n, # X-Werte (nicht Indizes) durchgehen
_K=K+1; # Spalten zählen, um Index für z zu bekommen
_if j=<0, # X-Werte kleinergleich 0 führt zu ..
__for L=1:n,
___z[L,K]=0; # .. setze alle Zeilenwerte in Spalte K gleich Null
__end
_elseif # Ansonsten berechne ..
__L=0;
__for i=a:e step (a-e-1)/n, # .. für Spalte K in jeweils allen Zeilen von 1 bis L den Wert z, wobei i der y-Wert ist
___L=L+1; # Index für Zeile
___z[L,K]=(2*j*i^2)/(j^2 + i^4); # funktioneller Zusammenhang
__end
_end
end

Ich hoffe, ich hab die Form jetzt richtig hingeschrieben. Der Code geht praktisch alle Werte auf der X- und Y-Achse ab, mit der gewählten Schrittweite. Diese Form macht praktisch die Arrays von X und Y überflüssig. Es reicht, die Dimension von x und y zu kennen, um das meshgrid zu erzeugen.

Ich sag's mal so - diese Form zu wählen ist weit weit weg von einem guten Algorhythmus. Was man glaub auch schon allein an der Form erkennt, die deutlich komplizierter aussieht, als die erste Form, die ich gepostet hatte.

Deine Berechnung von z stimmt nicht, du musst alle Operationen elementweise ausführen. Du hast da eine vergessen

Korrekt. Ich weiß ja nicht, ob MatLab das automatisch erkennt und ausführt, aber könnte es mir prinzipiell vorstellen, dass es den funktionellen Zusammenhang automatisch erkennt. Obwohl - aus mathematischer Sicht halte ich das für ziemlich ungelenk.
Dafür wäre dann mMn aber mindestens eine Vorabdefinition der Array-Dimension von z notwendig.

Wenn man das Ausrechnen der z-Matrix nicht elementweise ausführt, dann muss für die allgemeine Form z=f(x,y) die Bedingung erfüllt sein, dass x und y eindeutige Werte sind. In dem Fall sind es jedoch Vektoren. Insofern MatLab das nicht selbstständig abfängt, sollte das nicht zulässig sein.

Die Dimensionen von z werden durch meshgrid festgelegt (ein 2D-Netz in der xy-Ebene wird erstellt), durch z=... bekommt jede xy-Koordinate einen z-Wert.

Ich weiß ja nicht, ob ich das falsch verstehe, aber ich sehe programmtechnisch keinen funktionellen Zusammenhang, den meshgrid zwischen x,y und z herstellen würde.

Den grafischen Zusammenhang stellt die Funktion mesh (x,y,z) her. Aber das ist ja keine Berechnungsabhängigkeit.
Wenn du zwei Schleifen laufen lässt, ohne die Zählvariablen als Index oder Berechnungsvariable zu verwenden, ist das sinnlos.


Mal als bestes Beispiel: Du willst einen Code schreiben, um die Fakultät F einer Zahl m berechnen zu lassen. Der funktionelle ZUsammenhang lautet: F=m!

Zahl=m

F=1;
For i=1m-1)
_F=F*(F+1)
end

das klappt. Die andere Form wäre hier z.B.:

F=1;
for i=(1+1):m
_F=F*i
end

Ok - gleich lang in etwa. Erstere Form sieht etwas komplizierter aus, hat aber eine Wiederholung weniger.
Jetzt ändern wir die Aufgabe mal: Jetzt soll die Funktion F=m!-n! mit m>n>1 realisiert werden. Es wäre natürlich schwachsinnig, erst m!, dann n! zu berechnen und dann die Differenz zu bilden. Man multipliziert nur die Faktoren, die man brauch. In den zwei Formen kann man es so berechnen:

F=n;
For i=1m-n-1)
_F=F*(F+1)
end

Oder eben

F=n;
For i=(n+1):m
_F=F*i;
end

Unterschiede machen die Anzahl der Wiederholungen, die Anzahl der Summationen/Differenzen bzw. Multiplikationen.
Ein Informatiker wird dir sagen können, welcher Code besser ist. Also hinsichtlich der Übersichtlichkeit und der Schnelligkeit.

Wenn ich das richtig denke, ist der zweite Code schneller. Im ersten Code wird pro Wiederholung eine Muliplikation und eine Addition ausgeführt, dafür insgesamt eine Wiederholung weniger.
In der zweiten Form gibt es zwar eine Wiederholung mehr, aber dafür keine Addition.

Für eine steigende Anzahl an Wiederholungen ist somit der zweite Code effizienter und schneller. Nebenbei auch noch übersichtlicher.

Was ich damit sagen will: Keine Ahnung. Hauptsache es bleibt übersichtlich und du weißt, was der Code macht. Dazu gehört, dass man sich selbst ranschreibt, was welche Zeile eigentlich macht

ps: Da mein Beitrag jetzt etwas länger gebraucht hat: Was macht denn jetzt der Punkt???

 

[Müs Lee]

Zum Punkt: Dieser initiiert genau das, was du ansprichst - elementweise Operationen der Matrizen. Ohne Punkt wäre zB x*y eine normale Matrixmultiplikation.

Zu Meshgrid: Mir ist die Funktion selbst noch recht neu, aber ich probiers zu erklären.

Wie du hier siehst, wurden zwei Vektoren mit unterschiedlichen Dimensionen x und y erstellt. Meshgrid kopiert diese so oft wie benötigt und macht daraus zwei Arrays gleicher Dimension 10x5. In diesem speziellen Fall enthält Array X die x-Komponenten aller Koordinaten, Y die y-Komponenten (wer hätts gedacht). Mit z wird dann jedem xy-Paar die dritte Raumkoordinate zugewiesen. Mehr ist es an sich nicht, glaube ich.

Das sagt Matlab dazu:

>> help meshgrid
MESHGRID X and Y arrays for 3-D plots.
[X,Y] = MESHGRID(x,y) transforms the domain specified by vectors
x and y into arrays X and Y that can be used for the evaluation
of functions of two variables and 3-D surface plots.
The rows of the output array X are copies of the vector x and
the columns of the output array Y are copies of the vector y.

[X,Y] = MESHGRID(x) is an abbreviation for [X,Y] = MESHGRID(x,x).
[X,Y,Z] = MESHGRID(x,y,z) produces 3-D arrays that can be used to
evaluate functions of three variables and 3-D volumetric plots.

For example, to evaluate the function x*exp(-x^2-y^2) over the
range -2 < x < 2, -2 < y < 2,

[X,Y] = meshgrid(-2:.2:2, -2:.2:2);
Z = X .* exp(-X.^2 - Y.^2);
surf(X,Y,Z)

MESHGRID is like NDGRID except that the order of the first two input
and output arguments are switched (i.e., [X,Y,Z] = MESHGRID(x,y,z)
produces the same result as [Y,X,Z] = NDGRID(y,x,z)). Because of
this, MESHGRID is better suited to problems in cartesian space,
while NDGRID is better suited to N-D problems that aren't spatially
based. MESHGRID is also limited to 2-D or 3-D.

Class support for inputs X,Y,Z:
float: double, single

 

[InteGralFormat]

Versteh ich das mit dem Punkt richtig:

Man definiert:

x=(1 2)
y=(1 2 3)

[x,y]=meshgrid(x,y); --> erzeugt ein 2x3 = 6 Punkte Koordinatensystem mit den entsprechenden Wertebereichen bzw. Intervallen von x bzw. y

z=x.*y.

--> erzeugt automatisch die entsprechende Wertetabelle, OHNE dass man man irgendeine Schleife oder weitere Anweisungen braucht?

Z=
1 2 3
2 4 6

Na wenn das mal keine Programmierung für Faule ist
Und wie kann man dann auf einzelne Elemente zugreifen?


Ich hab grad versucht, dass ganze mal mit MathCad nachzubauen: Auswahl 3D-Plot, Funktion definiert, Axeneinstellungen gemacht und fertig



ok - das war glaub nicht der Sinn deiner Aufgabe, das so zu lösen

 

[Müs Lee]

Zum Punkt: ja korrekt, allerdings wäre es x.*y (ohne Punkt hinten, oder ist der in diesem Fall ein normales Satzzeichen?

Einzelne Elemente (oder auch mehrere oder gleich ganze Reihen) sind ganz einfach. Zum Beispiel

a=
1 2 3
4 5 6

Dann kann man mit a(2,2) auf die 5 zugreifen. Mit a(2,1:3) hätte man dann die Werte 4 5 6, sofern ich jetzt keinen Blödsinn geschrieben habe.

 

[Müs Lee]

[Nostalgie]
Hach, sieben Jahre ist das schon her. Wie die Zeit verfliegt... Aus Spaß habe ich die Aufgabe mal wieder ausgegraben, und mittlerweile geht das dann doch etwas leichter aus der Hand Vielleicht wird das 2028 noch etwas leichter.
[/Nostalgie]

clear all
clf
X = -10:0.1:10;
Y = X;

[x,y] = meshgrid(X,Y);
func = 2.*x.*y.^2 ./ (x.^2 + y.^4);
temp = func > 0;
func = temp.*func;

figure(1)
s=surf(X,Y,func)
xlabel('x'), ylabel('y'), zlabel('func')
axis square, rotate3d on, shading interp, colormap('Jet')