Hallo CB-Gemeinde,
ich habe eine Frage an Alle mit Kenntnis :-)
Ich möchte in Matlab die Verteilungsfunktion der Normalverteilung darstellen aber nicht wie sonst überlich als Integral von minus Unendlich bis x sondern umgekehrt.
Zuvor habe ich mir die Normalverteilung für verschiedene Sigmas und Mues plotten lassen. Leider kriege ich die Verteilungsfunktion mittels Integral nicht hin, sondern nur über normcdf.
Kann mir da jemand helfen?
Mein Code sieht so aus:
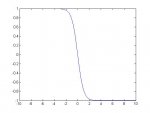
Mein Bild soll am ende etwa so aussehen wie y = -tanh(x) [siehe Plot], nur dass ich von sigma und mue abhängige Kurven Plotten will. Damit man den Einfluss sieht.
Danke im Voraus.
Zanmatou
ich habe eine Frage an Alle mit Kenntnis :-)
Ich möchte in Matlab die Verteilungsfunktion der Normalverteilung darstellen aber nicht wie sonst überlich als Integral von minus Unendlich bis x sondern umgekehrt.
Zuvor habe ich mir die Normalverteilung für verschiedene Sigmas und Mues plotten lassen. Leider kriege ich die Verteilungsfunktion mittels Integral nicht hin, sondern nur über normcdf.
Kann mir da jemand helfen?
Mein Code sieht so aus:
Code:
clc
clear all
sigma = [1 2 3]; % Varianz
mue = 0; % Erwartungswert
x = -10:0.01:10; % Wertebereich
for sigma = 1:length(sigma)
y = 1 /(sigma*(sqrt(2 * pi))) * exp((-1/2) * ((x-mue)/sigma).^2);
hold on
plot(x,y, 'r')
plot(x,normcdf(-10:0.01:10,mue,sigma))
endMein Bild soll am ende etwa so aussehen wie y = -tanh(x) [siehe Plot], nur dass ich von sigma und mue abhängige Kurven Plotten will. Damit man den Einfluss sieht.
Danke im Voraus.
Zanmatou