Servus,
ich habe vor 2 Tagen schon ein mal ein Thema zu meinem Programm eröffnet, das nun auch läuft, aaaber es gefällt mir noch nicht so ganz.
Ich habe ein Spiel programmiert, in dem man eine Zufallszahl erraten muss und ich habe die Aussage das die Zahl entweder zu groß oder zu klein ist.
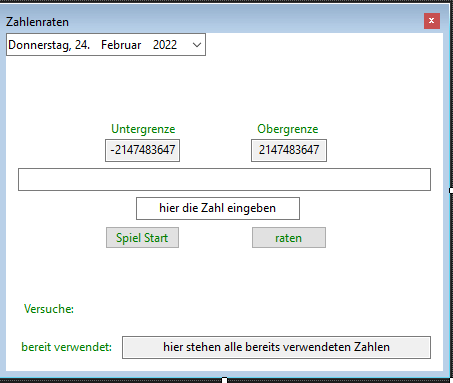
Nun möchte ich aber genauere Aussagen einbauen und die vorhandenen behalten. Also z. B., das Spektrum geht von -2147483647 bis 2147483647 und die Zufallszahl ist 0 dann kann bei 2147483647 stehen, dass die Zahl kleiner ist, aber wenn man z. B. 100 eintippt soll stehen das man nah dran ist aber die Zahl kleiner ist.
(Das Datum nicht beachten, das ist nur just for fun xD)
ich habe vor 2 Tagen schon ein mal ein Thema zu meinem Programm eröffnet, das nun auch läuft, aaaber es gefällt mir noch nicht so ganz.
Ich habe ein Spiel programmiert, in dem man eine Zufallszahl erraten muss und ich habe die Aussage das die Zahl entweder zu groß oder zu klein ist.
Nun möchte ich aber genauere Aussagen einbauen und die vorhandenen behalten. Also z. B., das Spektrum geht von -2147483647 bis 2147483647 und die Zufallszahl ist 0 dann kann bei 2147483647 stehen, dass die Zahl kleiner ist, aber wenn man z. B. 100 eintippt soll stehen das man nah dran ist aber die Zahl kleiner ist.
(Das Datum nicht beachten, das ist nur just for fun xD)
C#:
using System;
using System.Windows.Forms;
namespace Testproject
{
public partial class Form1 : Form
{
int obergrenze;
int untergrenze;
int zufallszahl = 0;
int counter = 0;
Random r = new Random();
public Form1()
{
InitializeComponent();
}
private void Form1_Load(object sender, EventArgs e)
{
}
private void button1_Click(object sender, EventArgs e)
{
lblversuche.Text = "";
textBoxEingabe.Text = "";
textBoxZähler.Text = "";
if (int.TryParse(textBox3.Text, out untergrenze))
{
if (int.TryParse(textBox4.Text, out obergrenze))
{
if (untergrenze < obergrenze)
{
zufallszahl = r.Next(untergrenze, obergrenze + 1);
textBoxAnzeige.Text = "Das spiel läuft";
}
else
{
textBoxAnzeige.Text = "Die Untergrenze muss kleiner als die Obergrenze sein";
}
}
else
{
textBoxAnzeige.Text = "Die Obergrenze muss eine gültige Zahl sein (1 - 10)";
}
}
else
{
textBoxAnzeige.Text = "Die Obergrenze muss eine gültige Zahl sein (1 - 10)";
}
}
private void button2_Click(object sender, EventArgs e)
{
int eingabe = 0;
counter += 1;
string Trennzeichen = " ";
lblversuche.Text = counter.ToString();
if (int.TryParse(textBoxEingabe.Text, out eingabe))
{
if (zufallszahl > eingabe)
{
textBoxAnzeige.Text = "Die Zufallszahl ist größer als die Eingabe";
}
else if (zufallszahl < eingabe)
{
textBoxAnzeige.Text = "Die Zufallszahl ist kleiner als die Eingabe";
}
else
{
textBoxAnzeige.Text = "Sie haben zwar gewonnen aber werden keinen Preis bekommen";
}
textBoxZähler.Text += Trennzeichen + eingabe.ToString();
}
else
{
textBoxAnzeige.Text = "Die Obergrenze muss eine gültige Zahl sein (1 - 10)";
}
}
private void textBox4_TextChanged(object sender, EventArgs e)
{
}
private void lblversuche_Click(object sender, EventArgs e)
{
}
private void textBox5_TextChanged(object sender, EventArgs e)
{
}
private void textBox1_TextChanged(object sender, EventArgs e)
{
}
private void textBox3_TextChanged(object sender, EventArgs e)
{
}
}
}
), würde der Versuch einer Lösung vor lauter Haare raufen eher früher als später zur vollständigen Glatze führen 
