JavaScript Parallelprojektion in perspektivische Projektion überführen

[CPU]

Hallo Community,

mit dem neuen HTML5 Canvas-Objekt habe ich in JavaScript einen wirklich einfachen Renderer für 3D Objekte erstellt. Hier ist er: Anhang anzeigen 3d_fin.html.txt. Die Rotation der Objekte mit der Maus ist noch nicht so hübsch, aber das kommt noch.

Auf jeden Fall möchte ich jetzt gerne diese Parallelprojektion in eine perspektivishe Projektion umwandeln. Also, dass das Bild für den Betrachter "natürlicher" aussieht. So (links die Parallelprojektion und rechts die gewünsche Projektion):


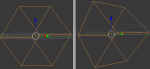
Aber im Netz kann ich kaum Ansatzpunkte finden, um meinen Renderer weiterzuentwickeln . Oder ich verstehe das alles falsch. Und daher erhoffe ich mir von Euch einen Anstoß wie ich weitermachen kann, um mein Ziel zu erreichen. Habt Ihr irgendwelche Ideen?

Viele Grüße,
CPU

 

[Nai]

Du benötigst eine homogene Division. Probier einfach mal:

 var FovY = (60*(Math.PI/180); // Blickwinkel entlang der Vertikalen; passt hoffentlich so
 var FovX = 2*atan(Aspect * tan(0.5*FovY)); // Blickwinkel entlang der horizontalen; passt hoffentlich so

 var TanFovX =  tan(0.5*FovX);
 var TanFovY =  tan(0.5*FovY);

 for (i = 0; i < vertices.length; i++) 
	{
        vertices[i].rotateX(angleX);
        vertices[i].rotateY(angleY);
        vertices[i].rotateX(angleZ);


       var XMax = TanFovX * vertices[i].z; // Diejenige Breite die in der Tiefe von vertices[i].z die "rechte Hälfte" des Bildschirms ausfüllt
       var YMax = TanFovY  * vertices[i].z; // Analog nur mit der Höhe


        var x1 = vertices[i].x/ XMax; //homogene Divison; 
        var y1 = vertices[i].y / YMax; // homogene Divison;

        var new_x = 0.5*(x1+1) * width;//Bildet den Wertebereich [-1, 1] auf [0, Width] ab
        var new_y = 0.5*(y1+1) * height;//Bildet den Wertebereich [-1, 1] auf [0, Height] ab
        as2D[i] = {x: new_x, y: new_y, };
    }

Wenn du dieses Vorgehen nicht verstehst, kann ich dir das auch mal aufmalen und einscannen.

Eigentlich müsste man bei der Berechnung von XMax und YMax noch schauen ob vertices.z von einem der beiden Eckpunkte der Gerade negativ ist und gegebenenfalls das geometrische Primitiv clippen. Denn so hast du hässliche Artefakte wenn die Gerade hinter Kamera verläuft. Deshalb gehört der gesamte Block nach den 3 Rotationsbefehlen nicht mehr zum Transformieren des Vertexes sondern zum Zeichnen einer Line.

P.S. verwende homogene Koordinaten; mit Eulerwinkeln stößt du sehr schnell an die Grenzen.

 

[CPU]

Hallo,

super vielen Dank Nai für den Code.

Wenn du dieses Vorgehen nicht verstehst, kann ich dir das auch mal aufmalen und einscannen.

Leider scheint es aber nicht den gewünschten Effekt zu haben, siehe hier: . Anscheinend verstehe ich Dein Vorgehen noch nicht so richtig, da ich nicht im Stande bin das Problem zu beheben.

Eigentlich müsste man bei der Berechnung von XMax und YMax noch schauen ob vertices.z von einem der beiden Eckpunkte der Gerade negativ ist und gegebenenfalls das geometrische Primitiv clippen. Denn so hast du hässliche Artefakte wenn die Gerade hinter Kamera verläuft.

Okay. Aber aus dem konkreten Szenario das mir vorschwebt weiß ich, dass die Kamera immer auf das "Modell" draufschaut und niemals Objekte hinter sich hat.

Viele Grüße,
CPU

 

[Nai]

Eben nocheinmal ein Blick auf deinen Quellcode geworfen. Die Rotate-Befehle dienen ja dazu, dass Koordinatensystem deines Würfels in das Koordinatensystem der Kamera zu transformieren. Da du nur rotierst, befindet sich das perspektivische Zentrum deiner Kamera im Kamerakoordinatensystem (0,0,0) stets auf dem einem Eckpunkt deines Würfels, da dieser ebenfalls immer bei (0,0,0) liegt. Das verursacht vermutlich das komische Aussehen. Probier mal stattdessen:

var Offset = 2;
var XMax = TanFovX * (vertices[i].z+Offset); // Diejenige Breite die in der Tiefe von vertices[i].z die "rechte Hälfte" des Bildschirms ausfüllt
var YMax = TanFovY * (vertices[i].z+Offset); // Analog nur mit der Höhe

 

[CPU]

Hallo,

Die Rotate-Befehle dienen ja dazu, dass Koordinatensystem deines Würfels in das Koordinatensystem der Kamera zu transformieren. Da du nur rotierst, befindet sich das perspektivische Zentrum deiner Kamera im Kamerakoordinatensystem (0,0,0) stets auf dem einem Eckpunkt deines Würfels, da dieser ebenfalls immer bei (0,0,0) liegt.

Verstehe.

Das verursacht vermutlich das komische Aussehen. Probier mal stattdessen:

Also kann ich mir das so vorstellen wie Fluchtpunktperspektive aus dem Kunstunterricht. Und mit "Offset" kann ich dann einstellen, wo dieser Fluchtpunkt liegt. Es sieht immer noch etwas merkwürdig aus (linke Seite):

Allerdings habe ich mir gedacht, dass bei einem Offset von -2 die Fluchtpunkte noch zu nah beieinander liegen und einfach mal erhöht (bzw. verkleinert) auf -4. Und das sieht doch (mit einigen Anpassung von near und far) recht ordentlich aus.

Danke für Deine Hilfe Nai!

Jetzt muss ich mich noch um eine ordentliche Rotation mit der Maus kümmern. Dazu habe ich noch eine Frage: also das Zeichen von Punkten und Linien ist unproblematisch und auch Faces kann ich recht gut (zumindest mit drei Punkten) einbauen - hatte ich auch schon testweise drin. Aber ich würde gerne wie in MeshLab so eine "Sphäre" hier (also einfach die zwei "Kreise") einbauen. Wie gehe ich dabei prinzipiell vor?

Klar ist, dass das ein 2D-Kreis ist der quasi über die 3D Darstellung gelegt wird und entsprechend gestaucht wird, damit es mit dem Modell zusammen räumlich aussieht. Aber den genauen Zusammenhang zu den Rotationswinkeln muss ich irgendwie identifizieren.

Viele Grüße,
CPU

 

[Nai]

Allerdings habe ich mir gedacht, dass bei einem Offset von -2 die Fluchtpunkte noch zu nah beieinander liegen und einfach mal erhöht (bzw. verkleinert) auf -4. Und das sieht doch (mit einigen Anpassung von near und far) recht ordentlich aus.

Ich hatte in meinem letzten Post einen vorzeichen Fehler drinnen. Nimm mal besser positive Werte für den Offset, da der Würfel sonst hinter der Kamera ist (was du aber wegen dem fehlenden Clipping nicht merkst).

Jetzt muss ich mich noch um eine ordentliche Rotation mit der Maus kümmern. Dazu habe ich noch eine Frage: also das Zeichen von Punkten und Linien ist unproblematisch und auch Faces kann ich recht gut (zumindest mit drei Punkten) einbauen - hatte ich auch schon testweise drin. Aber ich würde gerne wie in MeshLab so eine "Sphäre" hier (also einfach die zwei "Kreise") einbauen. Wie gehe ich dabei prinzipiell vor?

Ich würde den Kreis durch ein regelmässiges N-Eck approximieren, was sie wohl auch in dem Programm gemacht haben, wie man an den Ecken des "Kreises" erkennt. Das würde ich dann ersteinmal passend verschieben und dann immer mit den übrigen Vertexen mitrotieren lassen. Zeichnen kannst du das N-Eck ja dann so wie den Würfel.

Hierzu noch eine Anmerkung am Rande: Du transformierst bei jeder Rotation alle Vertexe deines Würfels (und überschreibst ihren alten Wert). Da der Würfel ein Festkörper ist, führt das mit der Zeit zu numerischen Ungenauigkeiten. Deshalb fässt man eigentlich die "Rohdaten" von einem Mesh bei seiner Bewegung nicht an, sondern man definiert eine Abbildung (homogene Koordinaten in den meisten Fällen), welche dessen Position beschreibt. Bewegt sich das Mesh, so aktualisiert man lediglich die Abbildung, nicht jedoch die Rohdaten selbst.

 

[CPU]

Hallo,

Ich würde den Kreis durch ein regelmässiges N-Eck approximieren, was sie wohl auch in dem Programm gemacht haben, wie man an den Ecken des "Kreises" erkennt. Das würde ich dann ersteinmal passend verschieben und dann immer mit den übrigen Vertexen mitrotieren lassen. Zeichnen kannst du das N-Eck ja dann so wie den Würfel.

achso. Ja das ist doch eigentlich recht simpel, die Kreise schon von Beginn an eingefügt zu haben und die werden dann wie ein normales Objekt behandelt ...

Hierzu noch eine Anmerkung am Rande: Du transformierst bei jeder Rotation alle Vertexe deines Würfels (und überschreibst ihren alten Wert). Da der Würfel ein Festkörper ist, führt das mit der Zeit zu numerischen Ungenauigkeiten. Deshalb fässt man eigentlich die "Rohdaten" von einem Mesh bei seiner Bewegung nicht an, sondern man definiert eine Abbildung (homogene Koordinaten in den meisten Fällen), welche dessen Position beschreibt. Bewegt sich das Mesh, so aktualisiert man lediglich die Abbildung, nicht jedoch die Rohdaten selbst.

Stimmt, wenn ich jetzt so darüber nachdenke. Aber das ist ja keine Arbeit ...

Viele Grüße,
CPU

 

[Nai]

Stimmt, wenn ich jetzt so darüber nachdenke. Aber das ist ja keine Arbeit ...

Das Problem wird nun dabei sein, dass die Rotation mit der Maus sich nicht mehr so verhalten wird, wie du es erwartest. Denn bislang hast du deine Vertexe immer relativ zur letzten Position über Eulerwinkel um eine bestimmte Achse rotiert, wofür sich die Eulerwinkel gut eignen. Nun willst du das ganze durch eine einzige Eulerwinkel-Transformation verwirklichen. In diesem Fall entspricht eine Rotation um einen bestimmten Winkel jedoch nicht mehr der Rotation um eine bestimmte Achse, wodurch sich das Rotieren mit der Maus schwieriger gestalten wird. Willst du das dann fixen, wäre es das einfachste die Eulerwinkel als Koordinatensystem aufzugeben.

 

[CPU]

Hallo,

Das Problem wird nun dabei sein, dass die Rotation mit der Maus sich nicht mehr so verhalten wird, wie du es erwartest.

Kein Problem: dann habe ich wenigstens noch etwas zu basteln :-)

aber noch eine Frage von mir: wenn ich ein Modell darstelle und die Faces zeichne kann man nur die Umrisse sehen. Ist ja klar, denn alle Faces haben die gleiche Farbe und es erscheint somit nur als eine 2D Figur. Und nun meine Frage: habt ihr eine Idee, wie ich eine ganz einfache Schattierung hinbekomme? Ich will jetzt keine großartige Sache mit Ausleuchtung und Schatten (dafür gibt es ja "richtige" 3D-Renderer bzw. Bibliotheken), nein einfach nur manche Faces dunkler darstellen und hierüber eine grundlegene Schattierung hinbekommen. Hättet Ihr da eine Idee?

Viele Grüße,
CPU

 

[Nai]

1. Wenn du deine Geometrie auffüllen möchtest, so benötigst du noch einen Z-Buffer um halbwegs richtige Ergebnisse zu erzielen. Denn ohne hängt die Endfrabe des Pixels von der Zeichenreihenfolge ab. Das Problem kannst du allerdings etwas "abmildern", indem du nur diejenigen Faces zeichnest, die Richtung Kamera schauen (Leicht anhand ihrer Normale bestimmbar) oder/und die Faces der Tiefe nach sortierst.

2. Einfaches Schattieren eines gesamten Dreiecks mit einer Farbe kannst du über Phong-Diffuse-Shading (http://en.wikipedia.org/wiki/Phong_reflection_model) hinbekommen:

//Der Code ist mit dem GLSL-Syntax geschrieben; musst du noch in deinen Syntax konvertieren
vec3 Lightvec = vec3(0,0,-1);
vec3 AmbientColor = vec3(0.4,0.4,0.4);
vec3 DiffuseColor = vec3(0.6,0.6,0.6);
vec3 Normal = normalize(cross(SecondCorner-FirstCorner,ThirdCorner-FirstCorner)); // Normale des Dreiecks oder des Vierecks
float LDotN = dot(Normal , Lightvec);
if(LDotN < 0)
    LDotN  = - LDotN; //Alternativ LDotN  = 0 in dieser Zeile verwenden dann sind Flächen dunkel wenn das Licht von hinten kommt.

vec3 TriangleColor = AmbientColor + LDotN  * DiffuseColor;

Mit TriangleColor kannst du dann das gesamte Dreieck einfärben. Wenn du die Berechnung für die untransformierten Vertexe anstellst, so kommt das Licht von einer bestimmten Richtung aus und bewegt sich nicht; Führst du diese Berechnung für die transformierten Vertexe aus, so wirkt es so, als ob du vorne an deiner Kamera eine Lichtquelle dranmontiert hättest.


Willst du aber Flächen mit Farbverläufen haben oder Glanzlichter bzw. SpecularHighlights oder einen Z-Buffer, so wirst du vermutlich nicht drum herumkommen, das geometrische Primitiv selbst zu rasterisieren oder irgendwelche APIs zu verwenden, welche es für dich übernehmen (OpenGL oder DirectX z.B.).

 

[CPU]

Hallo,

1. Wenn du deine Geometrie auffüllen möchtest, so benötigst du noch einen Z-Buffer um halbwegs richtige Ergebnisse zu erzielen. Denn ohne hängt die Endfrabe des Pixels von der Zeichenreihenfolge ab. Das Problem kannst du allerdings etwas "abmildern", indem du nur diejenigen Faces zeichnest, die Richtung Kamera schauen (Leicht anhand ihrer Normale bestimmbar) oder/und die Faces der Tiefe nach sortierst.

Das habe ich gelöst, indem ich die Faces der Tiefe nach sortiert habe.

Dein Code rettet mich mal wieder. Aber was ist "dot(Normal , Lightvec);" genau für ein Operator (Skalarprodukt?) und "TriangleColor" hat dann als Vektor drei Komponenten für RGB (jew. zwischen 0.0 und 1.0)?

Willst du aber Flächen mit Farbverläufen haben oder Glanzlichter bzw. SpecularHighlights oder einen Z-Buffer, so wirst du vermutlich nicht drum herumkommen, das geometrische Primitiv selbst zu rasterisieren oder irgendwelche APIs zu verwenden, welche es für dich übernehmen (OpenGL oder DirectX z.B.).

Das ist mir schon klar, dass die Bibliotheken vieeel ausgereifter sind, als das was ich bastele. Nur für meinem speziellen Fall kann ich die Bibliotheken nur schlecht gebrauchen.

Ich werde das gleich mal so umsetzen.

Gruß,
CPU

EDIT: es funktioniert wirklich super und "dot" ist anscheinend das Skalarprodukt. Tolles Ergebnis. Noch eine Frage: angenommen ich setze dieses kleine Projekt in einer "richtigen" Programmiersprache um (z.B. Java). Wie kann ich dann die Faces performant speichern bzw. im Speicher halten? Gibt es da eine passende Datenstruktur?

Außerdem frage ich mich, was genau near und fear machen. Ich habe die einfach mal so aus dem Netz übernommen und mit den Zahlen ein wenig herumgespielt bis die Ansicht gepasst hat. Ich würde aber gerne eine automatische Anpassung vornehmen, damit das Modell ganz im Bild ist und verstehe da den Zusammenhang nicht.

 

[Nai]

Das ist mir schon klar, dass die Bibliotheken vieeel ausgereifter sind, als das was ich bastele. Nur für meinem speziellen Fall kann ich die Bibliotheken nur schlecht gebrauchen.

Was willst du überhaupt machen, bzw. was genau spricht gegen Bibliotheken in deinem speziellen Fall?

Wie kann ich dann die Faces performant speichern bzw. im Speicher halten? Gibt es da eine passende Datenstruktur?

Was genau meinst du mit "Faces performant speichern"? Normalerweise sind sowohl deine Vertexe als auch deine Indexe in Arrays gespeichert, weil du mit diesem nur das machen willst wofür Arrays gut sind: Vom ersten zum letzten Element iterieren oder auf ein Element mit einem bestimmten Index zugreifen. Ähnlich verhält es sich mit deinem Framebuffer, in den du hineinzeichnest und bei welchem du auch per Index auf bestimmte Elemente zugreifen willst. Faces definiert man sich dadurch, dass man sagt jeweils n (3 beim Dreieck, 4 beim Quad) aufeinanderfolgende Vertex-Indexe im Index-Array definieren eine Face. Dadurch muss man bei dem Zeichnen einer Face nur über das Index-Array iterieren. Alternativ kannst du zusätzlich noch diverse andere Face-Attribute wie Farbe oder Anzahl der Vertexe bzw. Indexe in einem weiteren seperaten Array speichern über welches du beim Zeichnen ebenfalls iterierst.

Außerdem frage ich mich, was genau near und fear machen. Ich habe die einfach mal so aus dem Netz übernommen und mit den Zahlen ein wenig herumgespielt bis die Ansicht gepasst hat.

Es handelt sich um die Near bzw. um die Far-Plane des "Sichtvolumens" einer Standard-Rasterisierungskamera, bei welchem es sich um einen Pyramidenstumpf handelt:

Zur vollständigen Beschreibung des Volumens benötigt man noch die Width und die Heigth von der Near oder von der Far-Plane. Ursache für das eigenartige Sichtvolumen ist folgendes:
-Near und Far beschreiben wie sich die Tiefen-Werte der Kamera auf die Tiefen-Werte des Z-Buffers abbilden. Far-Plane bekommt den größten Tiefenwert, Near-Plane den kleinsten Tiefenwert.
-Nach der Projektion wird der Pyramidenstumpf auf den Einheitswürfel abgebildet. An diesem kann man leicht das Clipping vollstrecken.

In der von mir veränderten Version sollten jedoch allerdings Near und Far nichts mehr machen, da man die erst für das Clipping und den Z-Buffer benötigt. Bei dem Sichtvolumen von deiner Kamera handelt es sich deshalb auch um eine Pyramide und nicht um einen Pyramidenstumpf.

Ich würde aber gerne eine automatische Anpassung vornehmen, damit das Modell ganz im Bild ist und verstehe da den Zusammenhang nicht.

Um dafür zu sorgen, dass das Objekt komplett im Bild ist würde den "Offset" verändern. Denn dadurch bewegst du die Kamera vor und zurück. Dabei würde ich denjenigen "Offset" suchen, bei welchem der Z-Wert für alle transformierten Vertexe positiv ist und die homogene Division nur Ergebnisse im Bereich [-1,1] zurückgibt. Zusätzlich kannst du vor der homogenen Division und nach der Rotation noch einmal den X-Wert und den Y-Wert der Vertexe verändern. Dadurch bewegst sich die Kamera horizontal bzw. vertikal. Das Ziel sollte dabei sein dass der kleinste X-Wert und kleinste Y-Wert der homogenen Division in etwa -1 und der größte X-Wert und Y-Wert 1 sind.

 

[CPU]

Hallo und pardon für meine späte Antwort

Was willst du überhaupt machen, bzw. was genau spricht gegen Bibliotheken in deinem speziellen Fall?

Ich möchte eine statische Ansicht eines 3D-Modells erzeugen.

Um dafür zu sorgen, dass das Objekt komplett im Bild ist würde den "Offset" verändern. Denn dadurch bewegst du die Kamera vor und zurück. Dabei würde ich denjenigen "Offset" suchen, bei welchem der Z-Wert für alle transformierten Vertexe positiv ist und die homogene Division nur Ergebnisse im Bereich [-1,1] zurückgibt. Zusätzlich kannst du vor der homogenen Division und nach der Rotation noch einmal den X-Wert und den Y-Wert der Vertexe verändern. Dadurch bewegst sich die Kamera horizontal bzw. vertikal. Das Ziel sollte dabei sein dass der kleinste X-Wert und kleinste Y-Wert der homogenen Division in etwa -1 und der größte X-Wert und Y-Wert 1 sind.

Aber das hört sich nach probieren an und ist vielleicht nicht performant? Wie wäre es damit: man lässt sich einen Würfel anzeigen mit dem Volumen 1000 (also 10x10x10) und sieht zu, dass der in's Bild passt. Wenn man ein Modell nun lädt wird das auf 10 Skaliert und passt auch in die Ansicht herein.

Jetzt noch eine ganz andere Frage: also Faces zeichnen mit Belechtung funktioniert echt gut und sieht super aus . Den Z-Buffer habe ich hinbekommen (oder zumindest glaube ich, dass es sich um diesen handelt), indem ich die Faces einfach nach Durchschnitt der Z-Koordinaten sortiere. Ich würde allerdings gerne eine "Ebene" in das Modell legen die quasi alles durchschneidet und mit einem alpha-Wert eingefärbt ist (so dass man noch die Faces "darunter" sehen kann). Das habe ich probiert - es sieht aber echt merkwürdig aus und wird auch nicht richtig gezeichnet.

Habt Ihr da eine Idee?

Viele Grüße,
CPU

 

[Nai]

Ich möchte eine statische Ansicht eines 3D-Modells erzeugen.

Für so etwas empfiehlt es sich wirklich OpenGL (bzw. WebGL) zu verwenden, denn mit OpenGL geht das wesentlich einfacher und performanter.

Aber das hört sich nach probieren an und ist vielleicht nicht performant? Wie wäre es damit: man lässt sich einen Würfel anzeigen mit dem Volumen 1000 (also 10x10x10) und sieht zu, dass der in's Bild passt. Wenn man ein Modell nun lädt wird das auf 10 Skaliert und passt auch in die Ansicht herein.

Hört sich von der Idee her auch gut an.

Den Z-Buffer habe ich hinbekommen (oder zumindest glaube ich, dass es sich um diesen handelt), indem ich die Faces einfach nach Durchschnitt der Z-Koordinaten sortiere. Ich würde allerdings gerne eine "Ebene" in das Modell legen die quasi alles durchschneidet und mit einem alpha-Wert eingefärbt ist (so dass man noch die Faces "darunter" sehen kann). Das habe ich probiert - es sieht aber echt merkwürdig aus und wird auch nicht richtig gezeichnet.

Die Idee die Faces zu sortieren funktioniert nur fehlerfrei, wenn sich die Faces nicht jeweils gegenseitig "überlappen". Denn überlappen sie sich zwei Faces A und B, so sind Teile von B vor A und Teile von A vor B. Egal ob du nun A oder B zuerst zeichnest, in jedem Fall verdeckst du dann beim Zeichnen der letzteren Fläche Teile von der ersteren Fläche, welche eigentlich sichtbar sein sollten. Des Weiteren, falls man dei Faces lediglich nach ihren Schwerpunkt sortiert, treten sogar dann Fehler auf, wenn sich die Faces nicht überlappen.

Genau eine solche Überlappung hast du, wenn du eine transparente Ebene zeichnest. Denn hier sind nun Teile der Transparenten Ebene vor deinem Würfel, (in deinem Würfel?) und hinter deinem Würfel. (Nich vergessen: Sind Objekte wie diese Ebene hinter deiner Kamera, so erzeugt dies auch Bildfehler, da du kein Clipping durchführst)

Deshalb wirst du in diesem Fall nicht herum kommen selbst das geometrische Primitiv zu rasterisieren. Hier kannst du z.B. einen Algrotihmus von hier nehmen: http://www.sunshine2k.de/coding/java/TriangleRasterization/TriangleRasterization.html . Dann musst du noch die TiefenWerte perspektivisch korrekt innerhalb des Dreiecks interpolieren und einen einfachen Tiefentest vor dem Zeichnen in das Bild für jeden Pixel ausführen.

Hierzu noch eine Anmerkung am Rande: Tiefenbuffer funktionieren bei mehreren sich überlagernden Transparenzen im Allgemeinen nur "eingeschränkt" (siehe z.B. hier: http://www.sjbaker.org/steve/omniv/alpha_sorting.html)

 

[CPU]

Hallo,

Für so etwas empfiehlt es sich wirklich OpenGL (bzw. WebGL) zu verwenden, denn mit OpenGL geht das wesentlich einfacher und performanter.

ja, ja. Ich sehe es ein.

Nun das was ich in HTML5 gemacht habe war nur ein "Prototyp" (ich weiß auch nicht warum ich das gerade in HTML5 gemacht habe ...). Richtig soll das in Java laufen.

Allerdings habe ich mir mal die verfügbaren Bibliotheken angeschaut und denke, dass es auf Java3D hinauslaufen wird. Ich hätte zwar eine kleinere Bibliothek lieber gehabt, aber okay.

Ich bekomme es trotzdem partout nicht hin mit Java 3D mal ein Face aus drei Punkten anzuzeigen. Hättet Ihr gerade so mal ein Codebruchstück da liegen, anhand desse ich sehen kann wie man das macht? Es scheint mir ganz schön umständlich zu sein ...

Gruß,
CPU