Pol-Nullstellen-Diagramm, Verlauf der Ü-fkt bestimmen

[wurstmuffin]

Hallo Leute.

Schreibe morgen ne Klausur in GIV (Grundlangen Informationsverarbeitung) und bräuchte eure Hilfe. Wenn jemand IT studiert, hat er das wahrscheinlich schon durchgenommen.
Es geht wie es schon in der Überschrift steht um die Pol-Nullstellendiagramme.
Ich werde einfach nicht daraus schlau. In der Aufragenstellung werden Pol- und/oder Nullstellen angegeben und man soll daraus die Übertragungsfunktion ablesen. Seit Tagen sitzen meine Leute und ich daran, kommen da aber einfach nicht weiter.
Hier die Kurzfragen. Ab Kapitel 4 geht es da los.
Hoffe, jemand kann mit dabei helfen.

Danke
Gruß

 

[-oSi-]

Wann ist die Klausur ? Morgen ?

Du sagst doch selber, das du daraus nicht schlau wirst...
Da würde dir die Hilfe hier, sollte sie denn kommen, auch nicht weiterhelfen.
Das benötigt mehr Zeit, um verstanden zu werden.

 

[wurstmuffin]

erklähr mir lieber was die Pol und Nullstellen genau bewirken. Es ist nicht so, dass ich gerade mit dem Thema anfange, ich kann einfach das Puzzle nicht zusammensetzen, weil mir eben Kleinigkeiten fehlen. Wenn du das denn drauf hast, dann lös die Kurzfragen von Kap4 zu diesen Diagrammen. Ne kurze Beschreibung als erlärung würde mir schon weiterhelfen.

Die erste Frage: Das ist ein Hochpass, nur wie kommt man genau drauf? (s.B.)

 

[Morgoth]

Ist doch gar kein Thema:

aus den Polstellen lässt sich das Nenner-, aus den Nullstellen das Zählerpolynom der Übertragungsfunktion ablesen.

In der ersten Frage Deines PDFs wäre die Übertragungsfunktion dann also (Vorsicht, unter jedes w gehört normalerweise ein w1 als Konstante, das lass ich jetzt aber mal der Übersichtlichkeit wegen weg):

H(jw)=jw*jw / [(jw-(1+j)) * (-jw-(1-j)]

=> H(jw)=w² / [w²-1]

Davon der Betrag:

|H(jw)|=w² / [w²-1]

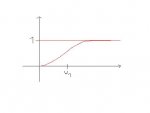
Bei w=0 ist die Amplitude also 0, bei w=inf. 1. Damit handelt es sich um einen Hochpass 2. Ordnung.

Das zweite ist schon ein bisschen doller, lassen wie am besten mal die Pol- und Nullstelle auf der reellen Achse weg. Das ergibt:

H(jw)=1 / [(jw-p) * (-jw-p)]

=> H(jw)=1 / [w²-p²]

Den Betrag davon solltest Du selber bilden können, das Verhalten ist ein Tiefpass zweiter Ordnung.

Fehlen noch jeweils eine Pol- und Nullstelle. Die beiden sind an der imaginären Achse gespiegelt, das heißt, diese beiden bilden einen Allpass, nennen wir ihn A(jw). Ein Allpass hat immer einen Amplitudenfrequenzgang von 1. Er hat also keinen weiteren Einfluss auf den Amplitudenfrequenzgang des Gesamtsystems (wohl aber auf den Phasenfrequenzgang!)

In der dritten Frage ist es ähnlich, ein Polstellenpaar wird in Kombination mit dem Nullstellenpaar zu einem Allpass, das andere Polstellenpaar bleibt übrig und bildet so einen Tiefpass 2. Ordnung.

Aufgabe 4 lässt sich genauso lösen.

Für Aufgabe 5 gebe ich Dir ein allgemeines Verfahren an, weil Du es ja nur skizzieren sollst.

Du solltest wissen, dass man Polstellen durch Nullstellen an der gleichen Stelle neutralisieren kann, und umgekehrt. Dann wird das jetzt offensichtlicher.

1.) Spiegelung der Nullstellen in der rechten Halbebene am Ursprung


2.) der minimalphasige Teil besteht aus den gespiegelten Nullstellen und den ursprünglichen Polstellen

3.) um den allpasshaltigen Teil der Ü-Fkt. zu erhalten, werden diese gespiegelten Nullstellen in Polstellen umgewandelt; der Allpass besteht dann aus den ursprünglichen Nullstellen und den neu gewonnenen Polstellen

Wenn Du nun beide PN-Pläne übereinander legst, liegen die gespiegelten Nullstellen und die daraus gewonnenen Polstellen genau aufeinander. Sie kompensieren sich damit, fallen also weg. Übrig bleibt der übsprüngliche Plan.

Aufgaben 6 und 7 solltest Du jetzt lösen können, dort will er die Ü-Fkt. als mathematischen Ausdruck. Weil beide Systeme allpasshaltig sind (Nullstellen rechts der imag. Achse) ist es schöner, die Ü-Fkt. in beide Teile aufzuspalten, also in der Form H(jw)=M(jw)*A(jw), wobei M(jw) der minimalphasige, A(jw) der allpasshaltige Teil ist.

Gruß
Morgoth

 

[wurstmuffin]

Hey, besten Dank. Wie Aufgabe 5) geht, steht zwar auch im Skript, aber danke für die Eklärung.
Bei Aufgabe 5 muss man ne Kleinigkeit beachten. Ich weiß jetzt nicht ob das ein Druckfehler ist oder so sein muss, denn bei einem Allpass müsste jeweils eine Nullstelle mit einer komlex konjugierten Pollstelle neutralisiert werden, sprich, man spiegelt die Nullstellen der rechten Halbebene an dem Achsenursprung, sprich Punktspiegelung. Nur wenn das so ist, dann ist Kurzfrage 4 falsch, denn da besteht der Allpassanteil aus nicht kunjugierten Null-Pollstellenpaaren, weißt du was ich meine? Schau hier auf Seite 32

Edit:
H(jw)=1 / [(jw-p) * (-jw-p)]

=> H(jw)=1 / [w²-p]

Muss das nicht H(jw)=1 / [w²-p²] sein? (p²)

 

[Morgoth]

Richtig, mein Fehler: nicht an der imag. Achse spiegeln, sondern am Ursprung.

Nur wenn das so ist, dann ist Kurzfrage 4 falsch, denn da besteht der Allpassanteil aus nicht kunjugierten Null-Pollstellenpaaren, weißt du was ich meine?

Nö, die ist richtig. Du hast den Allpass aus dem konjugiert komplexen Pol- und Nullstellenpaar und einen Tiefpass erster Ordnung durch die Polstelle auf der reellen Achse.

Nebenbei habe ich noch ein paar weitere Fehler in meinem Post ausgemerzt, hab das schon lang nicht mehr gemacht.

Gruß
Morgoth

 

[wurstmuffin]

dem Skript nach ist dem P01 der Poo1* gegenüber gestellt. In Aufgabe 4 stet dem Po1 der Poo1 gegenüber. Schau dir das mal genau an.

btw: hier, A4.2 kann man sich austoben

Besten DANK! Ich glaube, langsam verstehe ich das ganze Ich bin dir echt was schuldig!

 

[Morgoth]

Ja, aber das ist doch egal.

Das liegt nur an der Art, wie im Skript die Null- bzw. Polstellen erzeugt werden. Jeder Polstelle steht eine an der imag. Achse (sic!) gespiegelte Nullstelle gegenüber.

Und natürlich muss es p² heißen.

Gruß
Morgoth

 

[wurstmuffin]

in der Tat, is ja egal, ob * (also komplex konjugiert) oben oder unten ist, man weiß ja was gemeint ist.
Wenn das aber so ist, dann muss man es dann gar nicht Punktspiegeln, Achenspiegelung reicht doch dann auch aus?!

 

[Morgoth]

In diesen Fällen ja, aber es kann ja auch der Fall auftreten, dass nur eine einzige komplexe Nullstelle existiert. Dann muss es eine Punktspiegelung sein.

Gruß
Morgoth

 

[wurstmuffin]

alles klar, nach mal Danke für die schnelle Antwort
Kapitel 6 ist wohl das einige, was ich nicht so drauf habe, aber zum Bestehen sollte es reichen, hoffe ich...Morgen gehts um 08.30 Uhr los und gleich mal vier Stunden lang Macht aber trotzdem was. Ich wünsch dir noch einen schönen Abend