habichtfreak
Captain
- Registriert
- Aug. 2006
- Beiträge
- 3.618
1. Einleitung:
2. Wie werden Daten in der Informatik gespeichert:
3. Ein Rückblick in die Geschichte:
4.1 Umrechnung von Dezimal in Binär:
4.2.1 Umrechnung von Binär in Dezimal:
4.2.2 Umrechnung von Binär in Dezimal:
5 Sonderfälle
5.1 3 ½ Diskette
5.2 Speicher deren Kapazität tatsächlich geringer ist als angegeben
Ja, zu diesem Thema wurde schon viel geschrieben, auch der Wiki-Artikel versucht Licht ins dunkel zu bringen. Dennoch sind manche Artikel derart komplex geschrieben, dass diejenigen, die mit Informatik nicht so viel am Hut haben, schlicht überfordert sind. Ich möchte an dieser Stelle versuchen, mit so wenig wie möglichen und so viel wie nötigen Fachbegriffen zu erklären, warum Kapazitätsangaben abweichen, und niemanden das Gefühl beschleicht er müsse studiert haben um das geschriebene zu verstehen.
2. Wie werden Daten in der Informatik gespeichert:
Während der Mensch Zahlen, Zeichen und Buchstaben kennt, muss die Elektronik sich mit etwas weniger zufrieden geben, nämlich den beiden Ziffern 0 und 1. Die beiden Ziffern stehen stellvertretend für die Zustände LOW und HIGH. Wir Menschen arbeiten mit dem Dezimalsystem (Zehnersystem), in dem es 10 „verschiedene Zustände“ gibt, nämlich 0, 1, 2, … 8, und 9. Aus diesen 10 Ziffern lassen sich alle anderen Zahlen bilden, daher auch der Name Zehnersystem.
Ein PC kennt hingegen nur zwei Zustände, die durch die Zahlen 0 und 1 dargestellt werden. Daher heißt das verwendete Zahlensystem auch Dual- oder Binärsystem (dual = 2). Die kleinste Einheit in der Informatik ist das Bit, in dem entweder eine 0 oder eine 1 gespeichert sein kann. Die nächstgrößere Einheit ist das Byte, wobei ein Byte acht Bit entspricht.

Quelle: teach-ict.com
Nun ist es ein offenes Geheimnis, dass in der Informatik sehr große Datenmengen verarbeitet werden. Aus dem täglichen Leben kennen wir es bereits, sehr große Zahlen sind unhandlich und werden daher mit einem Präfix versehen. Z.B. ein Motor mit einer Leistung von 500.000 W.
Kilowatt (kW): 500* 103 --> 500 kW
Megawatt (MW): 0,5* 106 --> 0,5 MW
Würde man nach dem gleichen Schema versuchen 500.000 Byte mit einem Präfix zu versehen ergibt sich ein Problem, denn die Basis 10 gibt es nur im Dezimalsystem, aber nicht im Binärsystem. Dort gibt es die Basis 2. Die binäre Zahl die der 1000 (Umrechnungsfaktor im Dezimalsystem) am nächsten kommt ist 210 (1024). Diese relativ kleine Abweichung von 2,4% (24 von 1000) führt nicht selten zu großen Missverständnissen.
Ein PC kennt hingegen nur zwei Zustände, die durch die Zahlen 0 und 1 dargestellt werden. Daher heißt das verwendete Zahlensystem auch Dual- oder Binärsystem (dual = 2). Die kleinste Einheit in der Informatik ist das Bit, in dem entweder eine 0 oder eine 1 gespeichert sein kann. Die nächstgrößere Einheit ist das Byte, wobei ein Byte acht Bit entspricht.
Quelle: teach-ict.com
Nun ist es ein offenes Geheimnis, dass in der Informatik sehr große Datenmengen verarbeitet werden. Aus dem täglichen Leben kennen wir es bereits, sehr große Zahlen sind unhandlich und werden daher mit einem Präfix versehen. Z.B. ein Motor mit einer Leistung von 500.000 W.
Kilowatt (kW): 500* 103 --> 500 kW
Megawatt (MW): 0,5* 106 --> 0,5 MW
Würde man nach dem gleichen Schema versuchen 500.000 Byte mit einem Präfix zu versehen ergibt sich ein Problem, denn die Basis 10 gibt es nur im Dezimalsystem, aber nicht im Binärsystem. Dort gibt es die Basis 2. Die binäre Zahl die der 1000 (Umrechnungsfaktor im Dezimalsystem) am nächsten kommt ist 210 (1024). Diese relativ kleine Abweichung von 2,4% (24 von 1000) führt nicht selten zu großen Missverständnissen.
3. Ein Rückblick in die Geschichte:
Die Dezimalpräfixe (kilo, Mega, Giga, …) wurden anfangs auch für Byte-Angaben verwendet, was aufgrund der noch relativ kleinen Abweichungen „nicht weiter auffiel“. 1996 legte die IEC einen Entwurf für binäre Präfixe vor, die 3 Jahre später umgesetzt wurden. Diese Präfixe basieren auf den Dezimalpräfixen und enden auf -bi (für binär).
[table="width: 600, class: grid, align: center"]
[tr]
[td="colspan: 3"]
[td="colspan: 3"]
[/tr]
[tr]
[td]Kilobyte (KB)[/td]
[td]103[/td]
[td]1.000[/td]
[td]Kibibyte (KiB)[/td]
[td]210[/td]
[td]1.024[/td]
[/tr]
[tr]
[td]Megabyte (MB)[/td]
[td]106[/td]
[td]1.000.000[/td]
[td]Mebibyte (MiB)[/td]
[td]220[/td]
[td]1.048.576[/td]
[/tr]
[tr]
[td]Gigabyte (GB)[/td]
[td]109[/td]
[td]1.000.000.000[/td]
[td]Gibibyte (GiB)[/td]
[td]230[/td]
[td]1.073.741.824[/td]
[/tr]
[tr]
[td]Terabyte (TB)[/td]
[td]1012[/td]
[td]1.000.000.000.000[/td]
[td]Tebibyte (TiB)[/td]
[td]240[/td]
[td]1.099.511.627.776[/td]
[/tr]
[/table]
Der Tabelle kann man entnehmen, dass die Abweichungen mit zunehmender Kapazität größer werden. In der Informatik werden beide Zahlensysteme gleichzeitig verwendet, leider hat es sich 15 Jahre nach Einführung der Binärpräfix immer noch nicht durchgesetzt, beides strikt zu trennen oder besser gesagt, den richtigen Präfix zu verwenden. Daher hier eine kleine Liste wann welches Zahlensystem gemeint ist:
Dezimalpräfix in der Praxis:
Binärpräfix in der Praxis:
[table="width: 600, class: grid, align: center"]
[tr]
[td="colspan: 3"]
Dezimalpräfixe
[/td][td="colspan: 3"]
Binärpräfixe
[/td][/tr]
[tr]
[td]Kilobyte (KB)[/td]
[td]103[/td]
[td]1.000[/td]
[td]Kibibyte (KiB)[/td]
[td]210[/td]
[td]1.024[/td]
[/tr]
[tr]
[td]Megabyte (MB)[/td]
[td]106[/td]
[td]1.000.000[/td]
[td]Mebibyte (MiB)[/td]
[td]220[/td]
[td]1.048.576[/td]
[/tr]
[tr]
[td]Gigabyte (GB)[/td]
[td]109[/td]
[td]1.000.000.000[/td]
[td]Gibibyte (GiB)[/td]
[td]230[/td]
[td]1.073.741.824[/td]
[/tr]
[tr]
[td]Terabyte (TB)[/td]
[td]1012[/td]
[td]1.000.000.000.000[/td]
[td]Tebibyte (TiB)[/td]
[td]240[/td]
[td]1.099.511.627.776[/td]
[/tr]
[/table]
Der Tabelle kann man entnehmen, dass die Abweichungen mit zunehmender Kapazität größer werden. In der Informatik werden beide Zahlensysteme gleichzeitig verwendet, leider hat es sich 15 Jahre nach Einführung der Binärpräfix immer noch nicht durchgesetzt, beides strikt zu trennen oder besser gesagt, den richtigen Präfix zu verwenden. Daher hier eine kleine Liste wann welches Zahlensystem gemeint ist:
Dezimalpräfix in der Praxis:
- Optische Datenträger: DVD, BD // Ausnahme: CD
- Mechanische und flash-basierte Speichermedien: HDD, SSD, SD-Cards, USB-Sticks
- Übertragungsgeschwindigkeiten: Internet (z.B. 16.000 kbit/s); LAN (z.B. 100 Mbit/s)
Binärpräfix in der Praxis:
- Arbeitsspeicher
- Cache
- Flash-Speicherchips
- CDs
4.1 Umrechnung von Dezimal in Binär:
Das bekannteste Beispiel sind wohl Festplatten (HDDs), weshalb ich es an diesem erklären werde. Gegeben sei eine Festplatte die mit einer Kapazität von 1 TB verkauft wird. Nach dem Formatieren werden in Windows aber beispielsweise nur ~ 931 GB angezeigt. Diese Zahl kann man relativ einfach errechnen und prüfen ob die angezeigte Kapazität stimmt. Auch wenn es an dieser Stelle zu weit führt, ja es gibt Datenträger bei denen fehlt tatsächlich ein Teil der Kapazität.
1. Schritt: Umrechnen der Dezimalzahl in Byte
2. Schritt: Umrechnen von Byte in Binärzahl:
Damit haben wir die angezeigten 931 GB errechnet. Dummerweise zeigt Windows die Kapazität als binäre Zahl an, verwendet aber Dezimalpräfixe, denn eigentlich müsste es 931 GiB heißen. Damit nicht jeder den Taschenrechner zücken muss, hier mal ein Liste beliebter Festplattengrößen und deren Kapazitäten:
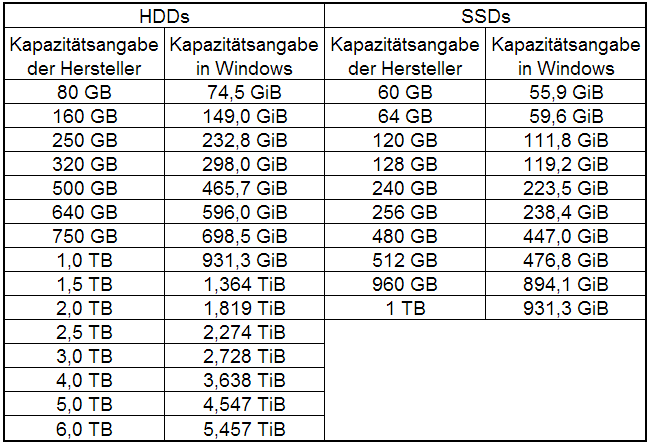
Anmerkung zur Kapazität von SSDs: Es hält sich hartnäckig das Gerücht, dass SSDs deren Kapazitäten sehr nah beieinander liegen, dieselbe Kapazität haben und einer der beiden Hersteller die Kapazität „ehrlich“ angibt. Gemeint sind die Kapazitäten 60 bzw. 64 GB, 120 bzw. 128 GB usw.
Ich kann nur mutmaßen wie es zu dieser These kam: Wahrscheinlich dachten die Leute eine 64 GB SSD hat 59,6 GiB und haben das mit 60 GB gleichgesetzt. Das ist Unfug, die nutzbare Kapazität unterscheidet sich um genau den Wert, den die Hersteller angeben, also 4 GB (60/64 GB), 8GB (120/128 GB) usw. Wer es nicht glaubt, kann sich gerne selbst überzeugen:
[table="width: 600, class: grid, align: center"]
[tr]
[td]
[td]
[/tr]
[tr]
[td]
 [/td]
[/td]
[td]
 [/td]
[/td]
[/tr]
[/table]
1. Schritt: Umrechnen der Dezimalzahl in Byte
- man multipliziert die angegebene Kapazität mit der Zahl für die der Präfix steht (siehe Tabelle oben)
- allgemein: Kapazität * 10x --> Kapazität in Byte
- Beispiel: 1 * 1012 --> 1.000.000.000.000 Byte
2. Schritt: Umrechnen von Byte in Binärzahl:
- man dividiert die errechneten Byte durch die Zahl für die der Präfix steht (siehe Tabelle oben)
- Allgemein: xxx Byte / 2y --> Kapazität in …bibyte
- Beispiel: 1.000.000.000.000 Byte / 230 --> 931,3 GiB
Damit haben wir die angezeigten 931 GB errechnet. Dummerweise zeigt Windows die Kapazität als binäre Zahl an, verwendet aber Dezimalpräfixe, denn eigentlich müsste es 931 GiB heißen. Damit nicht jeder den Taschenrechner zücken muss, hier mal ein Liste beliebter Festplattengrößen und deren Kapazitäten:
Anmerkung zur Kapazität von SSDs: Es hält sich hartnäckig das Gerücht, dass SSDs deren Kapazitäten sehr nah beieinander liegen, dieselbe Kapazität haben und einer der beiden Hersteller die Kapazität „ehrlich“ angibt. Gemeint sind die Kapazitäten 60 bzw. 64 GB, 120 bzw. 128 GB usw.
Ich kann nur mutmaßen wie es zu dieser These kam: Wahrscheinlich dachten die Leute eine 64 GB SSD hat 59,6 GiB und haben das mit 60 GB gleichgesetzt. Das ist Unfug, die nutzbare Kapazität unterscheidet sich um genau den Wert, den die Hersteller angeben, also 4 GB (60/64 GB), 8GB (120/128 GB) usw. Wer es nicht glaubt, kann sich gerne selbst überzeugen:
[table="width: 600, class: grid, align: center"]
[tr]
[td]
Corsair Force Series GT 120GB
[/td][td]
OCZ Octane SSD 128GB
[/td][/tr]
[tr]
[td]
[td]
[/tr]
[/table]
4.2.1 Umrechnung von Binär in Dezimal:
Der Arbeitsspeicher ist wohl den meisten Usern bekannt. Bei dem ist es genau umgekehrt zur Festplatte. Man kauft 8 GB und erhält etwas mehr, nämlich 8192 MB. Zumindest unter Windows wird dieser Wert angezeigt. Wieder liegt es am falschen Präfix, denn man kauft 8 GiB (Gibibyte). Da dieser Wert bereits binär ist, muss er nicht von einem Zahlensystem ins andere umgerechnet werden. Und damit ihr mir das nicht einfach nur glauben müsst, dass 8 GB eigentlich 8 GiB sind, rechne ich es an einem Beispiel vor. Dazu nehme ich den Kingston Value Ram DDR3-1600 (1 Modul). Der Hersteller gibt zu diesem Speicher folgendes an:
„This document describes ValueRAM's 1G x 64-bit (8GB) DDR3-1600 CL11 SDRAM (Synchronous DRAM) 2Rx8, memory module, based on sixteen 512M x 8-bit FBGA components.“
Auch wenn man der englischen Sprache mächtig ist, klingt das doch erst mal nach Bahnhof. Das Speichermodul ist aus 16 Speicherchips aufgebaut, von denen jeder 512Mx8-bit speichern kann. Das klingt nach einer komischen Größenangabe, ist aber nur eine andere Schreibweise. Was sich dahinter verbirgt: 512 M steht für 512 Mebi (ohne Bit oder Byte), also 536.870.912 [Einheitenlos] (512*220). Diese Zahl wird mit 8 bit multipliziert (…x 8-bit) und durch 8 dividiert (damit aus Bit Byte wird). Die beiden achten kann man gegeneinander kürzen und es bleibt die Einheit Byte über. Damit hat jeder der 16 Chips 536.870.912 Byte, zusammen also 8.589.934.592 Byte. Diese Größe kann man nun wahlweise in Dezimal oder Binär umrechnen:
Binär (GiB): 8.589.934.592 Byte / 230 --> 8 GiB
Binär (MiB): 8.589.934.592 Byte / 220 --> 8.192 MiB
Dezimal (GB): 8.589.934.592 Byte / 109 --> ~8,589 GB
Dezimal (MB): 8.589.934.592 Byte / 106 --> ~8.589 MB
Die dezimale Größe des Arbeitsspeichers steht hier nur der Vollständigkeit halber. In der Praxis wird für RAM ausschließlich das Binärsystem verwendet.
„This document describes ValueRAM's 1G x 64-bit (8GB) DDR3-1600 CL11 SDRAM (Synchronous DRAM) 2Rx8, memory module, based on sixteen 512M x 8-bit FBGA components.“
Auch wenn man der englischen Sprache mächtig ist, klingt das doch erst mal nach Bahnhof. Das Speichermodul ist aus 16 Speicherchips aufgebaut, von denen jeder 512Mx8-bit speichern kann. Das klingt nach einer komischen Größenangabe, ist aber nur eine andere Schreibweise. Was sich dahinter verbirgt: 512 M steht für 512 Mebi (ohne Bit oder Byte), also 536.870.912 [Einheitenlos] (512*220). Diese Zahl wird mit 8 bit multipliziert (…x 8-bit) und durch 8 dividiert (damit aus Bit Byte wird). Die beiden achten kann man gegeneinander kürzen und es bleibt die Einheit Byte über. Damit hat jeder der 16 Chips 536.870.912 Byte, zusammen also 8.589.934.592 Byte. Diese Größe kann man nun wahlweise in Dezimal oder Binär umrechnen:
Binär (GiB): 8.589.934.592 Byte / 230 --> 8 GiB
Binär (MiB): 8.589.934.592 Byte / 220 --> 8.192 MiB
Dezimal (GB): 8.589.934.592 Byte / 109 --> ~8,589 GB
Dezimal (MB): 8.589.934.592 Byte / 106 --> ~8.589 MB
Die dezimale Größe des Arbeitsspeichers steht hier nur der Vollständigkeit halber. In der Praxis wird für RAM ausschließlich das Binärsystem verwendet.
4.2.2 Umrechnung von Binär in Dezimal:
Ein weiteres sehr bekanntes Beispiel ist die CD. Obgleich es verschiedene Kapazitäten gibt, in diesem Beispiel beziehe ich mich nur auf den Standardrohling der als „700 MB“ verkauft wird. Auch in diesem Fall ist der Präfix falsch, denn der Rohling hat 700 MiB. Analog zur bereits bekannten Umrechnung, wandelt man die binäre Kapazität in Byte um und anschließend in dezimal:
1. Schritt:
2. Schritt:
Anmerkung: DVD und BD Rohlinge können nach diesem Schema nicht umgerechnet werden, da die angegebene Kapazität in Gigabyte (GB) auch tatsächlich für Gigabyte steht. Der Vollständigkeit halber auch hier die Kapazitäten für diese Rohlinge:

1. Schritt:
- 700 MiB (Mebibyte) --> 700 * 220 Byte --> 734.003.200 Byte
2. Schritt:
- 734.003.200 Byte / 106 --> ~ 734 MB (Megabyte)
Anmerkung: DVD und BD Rohlinge können nach diesem Schema nicht umgerechnet werden, da die angegebene Kapazität in Gigabyte (GB) auch tatsächlich für Gigabyte steht. Der Vollständigkeit halber auch hier die Kapazitäten für diese Rohlinge:
5 Sonderfälle
5.1 3 ½ Diskette
Die klassische „1,44 MB“ Diskette hatte eine sehr abenteuerliche Kapazitätsangabe, denn um auf besagte 1,44 MB (Megabyte) zu kommen, muss man eine binäre Zahl bewusst falsch umrechnen. Unabhängig vom Zahlensystem, kann man die Kapazität einer Diskette ganz leicht in Byte berechnen. Bei der 3 ½ Diskette sind es 512 Byte * 18 (Sektoren) * 80 (Spuren) * 2 (High Density) = 1.474.560 Byte. Rechnet man dies nun in Kibibyte um, ergeben sich 1.440 KiB (1.474.560 Byte / 210). Diese binäre Zahl hat man dann durch 1000 (103) geteilt um auf besagte 1,44 MB zu kommen. Das man so nicht umrechnet, hat hoffentlich jeder verstanden. Richtig wäre neben 1.440 KiB auch 1,406 MiB, 1.474 KB oder 1,474 MB.
5.2 Speicher deren Kapazität tatsächlich geringer ist als angegeben
Egal um welches Gerät es sich handelt, rechnet man die Kapazität in Byte um, also ohne Präfix, dann muss diese Zahl mindestens der Herstellerangabe entsprechen.

Auf dem Bild ist die Kapazität einer „2 TB“ HDD unter Windows zu sehen. Für gewöhnlich haben Datenträger nicht exakt diese Größe (in diesem Fall wären es 2.000.000.000.000 Byte) sondern ein bisschen mehr (weniger als 1%). Die von Windows angezeigten „1,81 TB“ sind wertmäßig richtig, aber der Präfix ist falsch (Siehe 4.1). Aber es gibt auch Datenträger deren Kapazität ist geringer als angegeben.

Auf diesem Bild sieht man die Kapazitätsangabe unter Windows. Es handelt sich um einen „64 GB“ USB-Stick, der mindestens 64.000.000.000 Byte haben muss. Tatsächlich sind es über 750.000.000 Byte (750 MB oder 715 MiB) zu wenig. Das sind zwar nur 1,2% zu wenig, aber es dürfte nicht sein. Glücklicherweise passiert das sehr sehr selten.
Auf dem Bild ist die Kapazität einer „2 TB“ HDD unter Windows zu sehen. Für gewöhnlich haben Datenträger nicht exakt diese Größe (in diesem Fall wären es 2.000.000.000.000 Byte) sondern ein bisschen mehr (weniger als 1%). Die von Windows angezeigten „1,81 TB“ sind wertmäßig richtig, aber der Präfix ist falsch (Siehe 4.1). Aber es gibt auch Datenträger deren Kapazität ist geringer als angegeben.
Auf diesem Bild sieht man die Kapazitätsangabe unter Windows. Es handelt sich um einen „64 GB“ USB-Stick, der mindestens 64.000.000.000 Byte haben muss. Tatsächlich sind es über 750.000.000 Byte (750 MB oder 715 MiB) zu wenig. Das sind zwar nur 1,2% zu wenig, aber es dürfte nicht sein. Glücklicherweise passiert das sehr sehr selten.
Anhänge
Zuletzt bearbeitet: