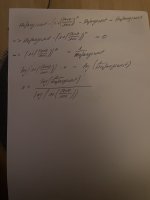PHP Für Rätselfreunde mit Hang zur Mathematik [PHP]

[MrStools]

Hallo, schön, dass du dir das ansiehst!
Vorab: Es geht hier nur um meine Neugierde. Es ist nichts wichtiges und ich möchte niemandem die Zeit stehlen.

Ein Freund hat mir eine Frage gestellt und ich kann das Problem zwar per Programm/Schleife lösen, ihm aber keine mathematische Formel geben, die das gewünschte Ergebnis liefert, obwohl das möglich sein muss.
Es geht um eine Zinseszinsproblematik. Wie oft muss verzinst werden nach folgendem Schema, bis ich gleich viel oder mehr Zinsen habe, wie mein Anfangswert.
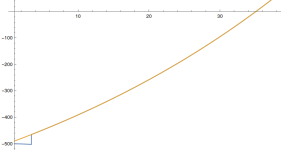
Ich habe eine Summe, die mit einem festen Zinssatz verzinst wird. Und das geht so: Es wird verzinst. Ist die Summe der Zinsen höher als ein Schwellwert, dann werden der Anfangssumme die bisher angefallenen Zinsen hinzuaddiert (nur dann). Wenn nicht, dann werden die Zinsen "gesammelt". Bei einem Anfangswert von 500€ und 2% Zinsen bräuchte ich also 4 "Runden" (jeweils 10€), um den Schwellwert (35€) zu überschreiten. Nun hätte ich 540 € und in der nächsten Runde würden 10.80€ Zinsen anfallen, die aber unter der Schwelle liegen, also würde das wiederholt, usw. Um im Beispiel zu bleiben, nach 36 Runden hätte ich einen Betrag an Zinsen "verdient", der die Anfangssumme übersteigt.
Ich suche jetzt eine allgemeine Formel, in die ich Anfangswert, Zinssatz und Schwellwert einsetze und die mir dann sagt, wie oft verzinst werden muss.
Hast du Lust (und die Fähigkeit), das für mich zu lösen?
Und als ob das nicht genug wäre, hätte ich gerne diese Formel in PHP-Notation.
Danke vielmals.
Was nicht nötig ist (aber natürlich die Sahne wäre, vor allem für andere, die sich hierher verirren), wäre eine Erklärung der Formel.
Nochmals danke.
Und wenn du sagst, ich mache doch keine Hausaufgaben für dich, auch gut. Wie gesagt, das ist mehr ein Spaß unter Freunden und es ist keine Hausaufgabe.
Hab ich mich schon bedankt?

 

[DieRenteEnte]

Anstatt dir eine Lösung zu geben, habe ich deine Frage einfach ChatGPT gestellt (Copy & Paste) und folgende Quellen dazu erhalten.

• Eins
• Zwei
• Drei
• Vier
• Fünf
• Sechs

Warum? Weil es für mich 100 % wie eine Hausaufgabe aussieht...
Ich hätte dir eine Lösung geschrieben, wenn du nur einen Teil davon nicht verstehen würdest oder 1-2 spezifische Fragen gestellt, aber die Mühe / Vorarbeit für den Rest gezeigt hättest.

 

[MrStools]

Nein, es ist keine Hausaufgabe. Ich habe schlichtweg schon einige Zeit damit verbracht ohne es lösen zu können, also ohne eine funktionierende Formel herauszubekommen (ich habe es auch mit ChatGPT versucht). Mathe war zwar mal mein Lieblingsfach, aber das ist lange her. Und ich muss momentan einige wichtigere Dinge erledigen. Wenn das niemand für mich macht, ist das in Ordnung. Wenn aber doch würde es mich sehr freuen. Und vielleicht ja auch andere.

 

[Enotsa]

https://www.mathebibel.de/zinseszinsformel#beispiel-4

Die müsste es doch sein oder...

 

[MrStools]

@Enotsa Nein, denn so einfach ist es ja nicht, durch das komische System.

 

[Nilson]

Durch deine binäre Abfrage (großer oder kleiner Schwelle) bin ich der Meinung, dass es dafür keine allgemeine Formel gibt. Du kannst höchsten pro Stufe ausrechnen wie viele Zyklen es bis zur nächsten sind.

 

[Enotsa]

Ich suche jetzt eine allgemeine Formel, in die ich Anfangswert, Zinssatz und Schwellwert einsetze und die mir dann sagt, wie oft verzinst werden muss.

Liest sich aber so. Wenn es dann nach der Schwellwerterreichung noch weitere Runden geben soll musst du halt eine Logik dafür programmieren. Aber für die Berechnung der Runden, dauer oder was auch immer sollte die Formel eine Grundlage sein.

 

[MrStools]

Wie @Nilson schon sagt, vermutlich kann man per Formel nur die "Runden" bis zum Erreichen der Schwelle in eine Formel packen und braucht für den Rest eine Logik, wie du sagst @Enotsa .

 

[Skysurfa]

Probier das mal ob das so hinkommt. Mathe ist bei mir auch schon ein paar Jahre her.

 

[MrStools]

@Skysurfa Danke für die Mühe, aber da taucht ja nirgends dieser Schwellwertkäse auf, also kann das in meinem Augen nicht die gewünschte Lösung sein (aber ein Teil davon schon!)

 

[Nilson]

@Skysurfa zum einen ist deine erste Zeile falsch, zum anderen ist es das, was @Enotsa schon vorgeschlagen hat. Leider kommt man hier mit klassischem Zinseszins nicht weiter.

 

[Skysurfa]

Ach… Ich hab das mit dem Schwellwert nicht ganz geblickt… Kleinen Moment. Ich pass das mal an. Wird aber eine rekursive Geschichte.

 

[Superior1337]

In meinen Augen ist die Aufgabenstellung nicht lösbar. In einer Formel diese while condition einzubauen mit dem Schwellenwert... also mathematisch vielleicht möglich wenn man die Zinseszinsformel nimmt, zur Laufzeit, umschreibt und mit dem Summenzeichen (Sigma) rekursiv aufaddiert bis als Grenze eine Ungleichung (< Schwellenwert) gegeben ist und dann nochmal das gleiche mit einem zweiten Summenzeichen, bis der Grundbetrag überschritten wird und so weiter. Aber das ist dann letztlich auch nur "eine Formel", weil die Logik auf Papier in eine Zeile gepresst ist und will man das in eine Programmiersprache wie PHP übertragen, dann kommt da immer eine while condition drin vor, wo man dann eben einen Zähler iteriert.

Der Sinn erschließt sich mir nicht, warum es wie vorgegeben gelöst werden MUSS.

Das ist ja so, als wenn ich einen Nagel in die Wand hauen soll, einen Hammer habe, aber nur mit den Stil auf den Nagel hauen darf.

 

[Skysurfa]

So in der Richtung müsste das klappen. Denke ich…

 

[MrStools]

Ich glaube wir haben einen Zustand erreicht, an dem wir uns alle entspannen dürfen. Es ist wohl klar geworden, dass es eine solche Formel nicht geben kann und wie gesagt, als Programm liegt es bereits vor und läuft. So bin ich ja auf die 36 gekommen. Ich danke euch und weiß eure Mühe wirklich zu schätzen!

 

[Schwachkopp]

Zumindest approximativ sollte da schon was gehen. Folgende Angaben sind ohne Gewähr. Für die normale Zinseszinsrechnung gilt

wobei A das Startkapital ist, S das Endkapital nach n Verrechnungen und p der Zinssatz (Groß P ist nur eine nützliche Abkürzung).

Nun brauchen wir noch die Summe der Zinsen:

Es fehlt noch eine Funktion, die die vom OP formulierte Sprungbedingung berücksichtigt:

Θ ist die Heaviside-Funktion (siehe Link unten), welche sich auch durch andere "normale" Funktionen annähern ließe, aber das lassen wir an der Stelle sein. T (für Threshold) sei der Schwellwert. Wenn jetzt die Summe der Zinsen größer als der Schwellwert wird, dann wird das Argument von Θ positiv und die Heaviside-Funktion nimmt den Wert 1 an, d.h. es steht dann Z*1 da, anonsten ist es 0.

Das Teil hauen wir nun oben in die Gleichung für den Zinseszins rein (genauer gesagt muss das zum Vorfaktor A addiert werden) und beachten noch, dass nur beim Überschreiten der Schwelle die Zinsen hinzuaddiert werden:

S' hat für n=36 den Wert 1000 bzw. etwas darüber. Leider lässt sich das nicht ohne weiteres nach n umstellen (hab auch keine große Motivation es zu versuchen), so dass nur approximieren oder plotten bleibt.

Wenn man noch ein bisschen daran herumbastelt sieht man, es muss

gelten. Geplottet sieht man wieder, dass n=36 sein muss:

Eigentlich hatte ich eine rekursive Formel erwartet, die man dann evtl. in eine explizite Form umwandeln hätte können aber irgendwie gehts scheinbar auch einfach so.

@MrStools Bist du sicher, dass 36 korrekt ist? Es wundert mich, dass nur ein Sprung in meinem Plot zu sehen ist; u.U haben wir beiden einen (denselben) Fehler gemacht.

https://en.wikipedia.org/wiki/Heaviside_step_function

Edit:
Der Clou ist, es kommt auch ohne den ganzen Schwellwertkram n=36 heraus. Denke das da oben ist unvollständig und man sollte tatsächlich eine rekursive Formel erhalten. Man muss dafür einfach obige Schritte immer wieder ausführen. Also Mit S' kann man ein Z' berechnen und daraus dann ein S'' usw.

Vermutlich bekommt die Funktion bei Berücksichtigung der Schwellen einen treppenartigen Verlauf, der einfachen Zinseszins-Funktion folgend. Der Wert von n wird nur unterschiedlich sein, wenn der Schnittpunkt zur x-Achse ungünstig liegt. Die blaue Funktion von oben ist durch die Zinseszins-Funktion verdeckt:

So genug Zeit hierauf verschwendet.^^