MKL Tweak auf Ryzen Systemen verbessert die Leistung drastisch

cm87 · 17. Dezember 2019

Spät aber doch:

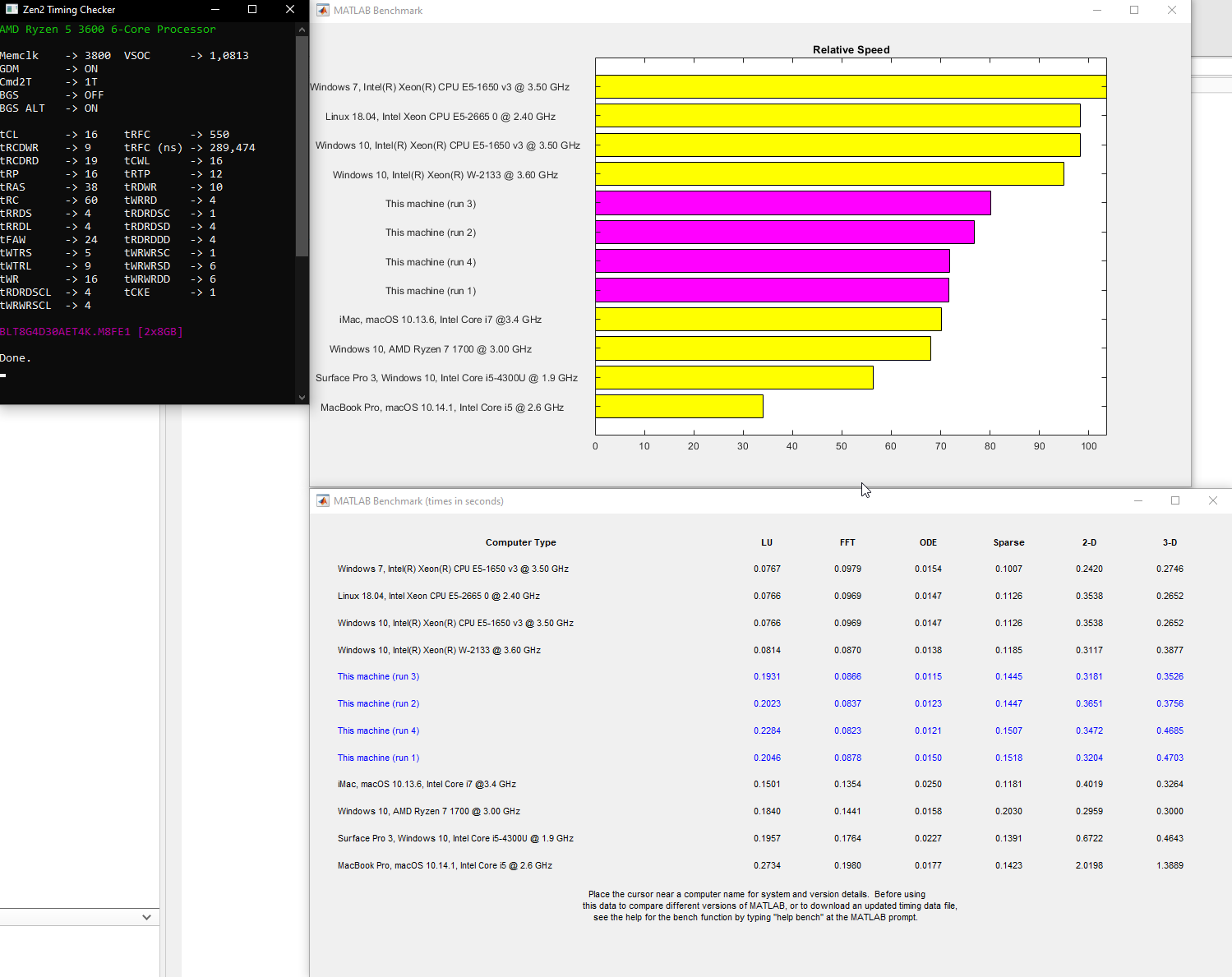
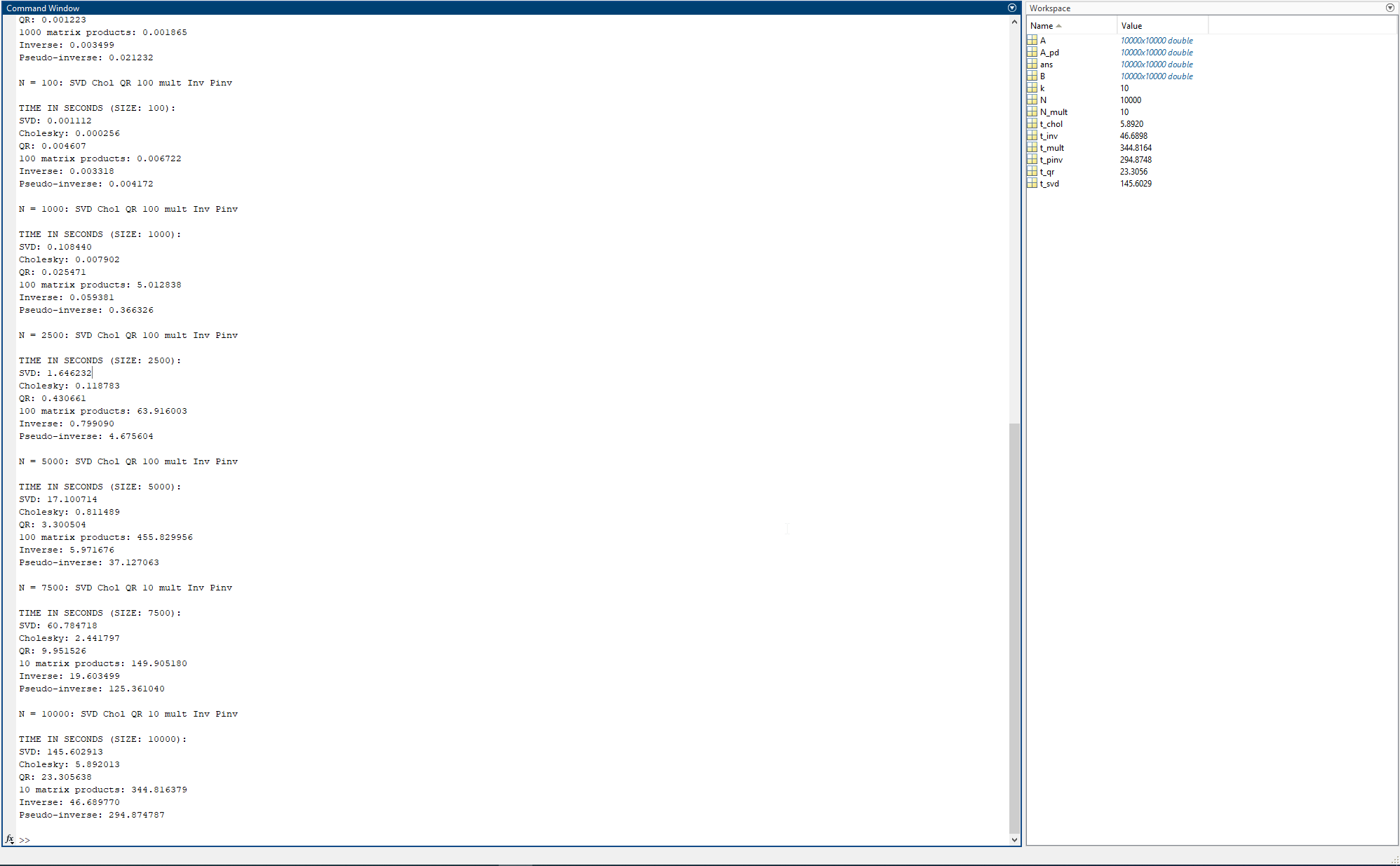
N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.050341
Cholesky: 0.001806
QR: 0.001223
1000 matrix products: 0.001865
Inverse: 0.003499
Pseudo-inverse: 0.021232

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.001112
Cholesky: 0.000256
QR: 0.004607
100 matrix products: 0.006722
Inverse: 0.003318
Pseudo-inverse: 0.004172

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.108440
Cholesky: 0.007902
QR: 0.025471
100 matrix products: 5.012838
Inverse: 0.059381
Pseudo-inverse: 0.366326

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 1.646232
Cholesky: 0.118783
QR: 0.430661
100 matrix products: 63.916003
Inverse: 0.799090
Pseudo-inverse: 4.675604

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 17.100714
Cholesky: 0.811489
QR: 3.300504
100 matrix products: 455.829956
Inverse: 5.971676
Pseudo-inverse: 37.127063

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 60.784718
Cholesky: 2.441797
QR: 9.951526
10 matrix products: 149.905180
Inverse: 19.603499
Pseudo-inverse: 125.361040

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 145.602913
Cholesky: 5.892013
QR: 23.305638
10 matrix products: 344.816379
Inverse: 46.689770
Pseudo-inverse: 294.874787

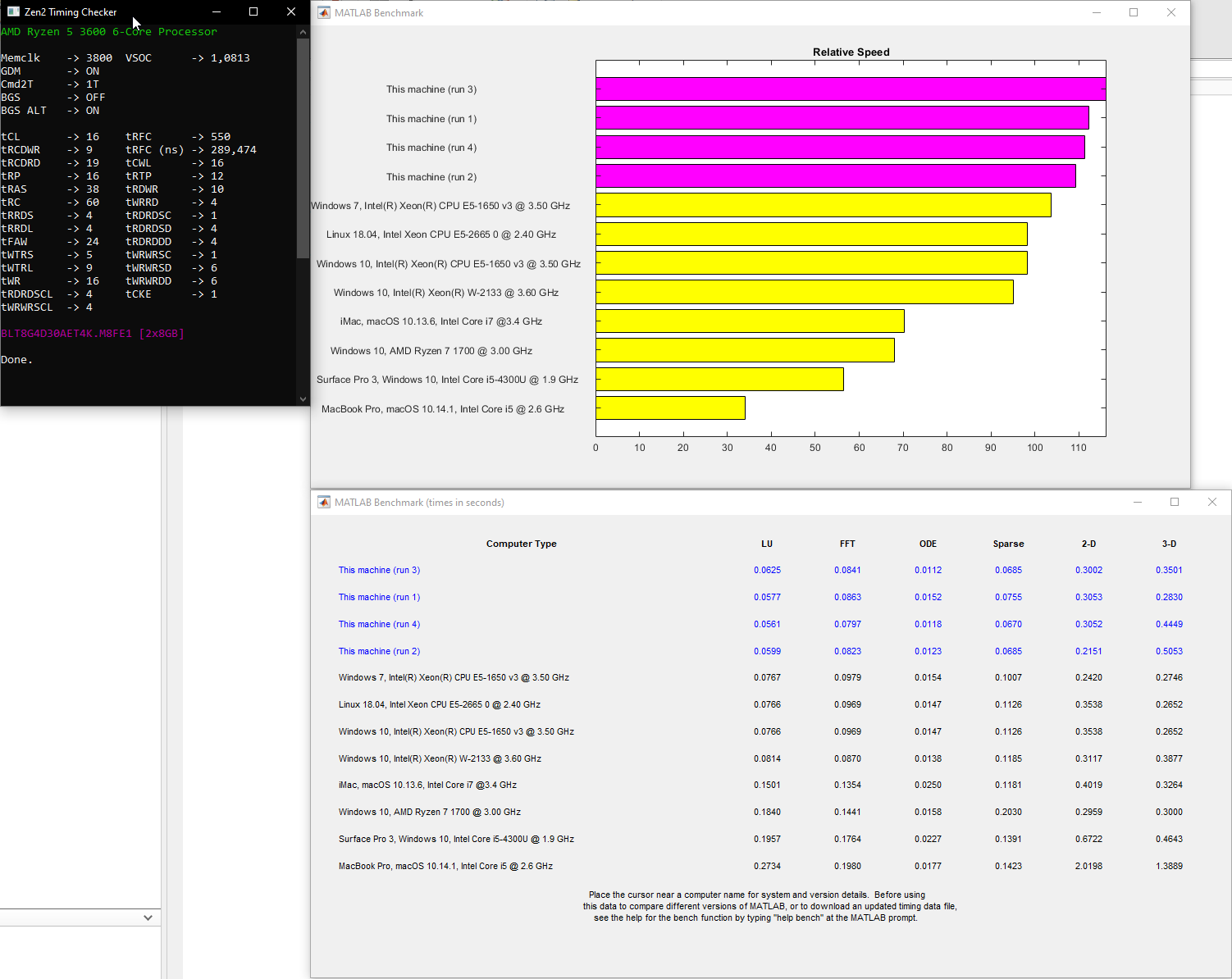
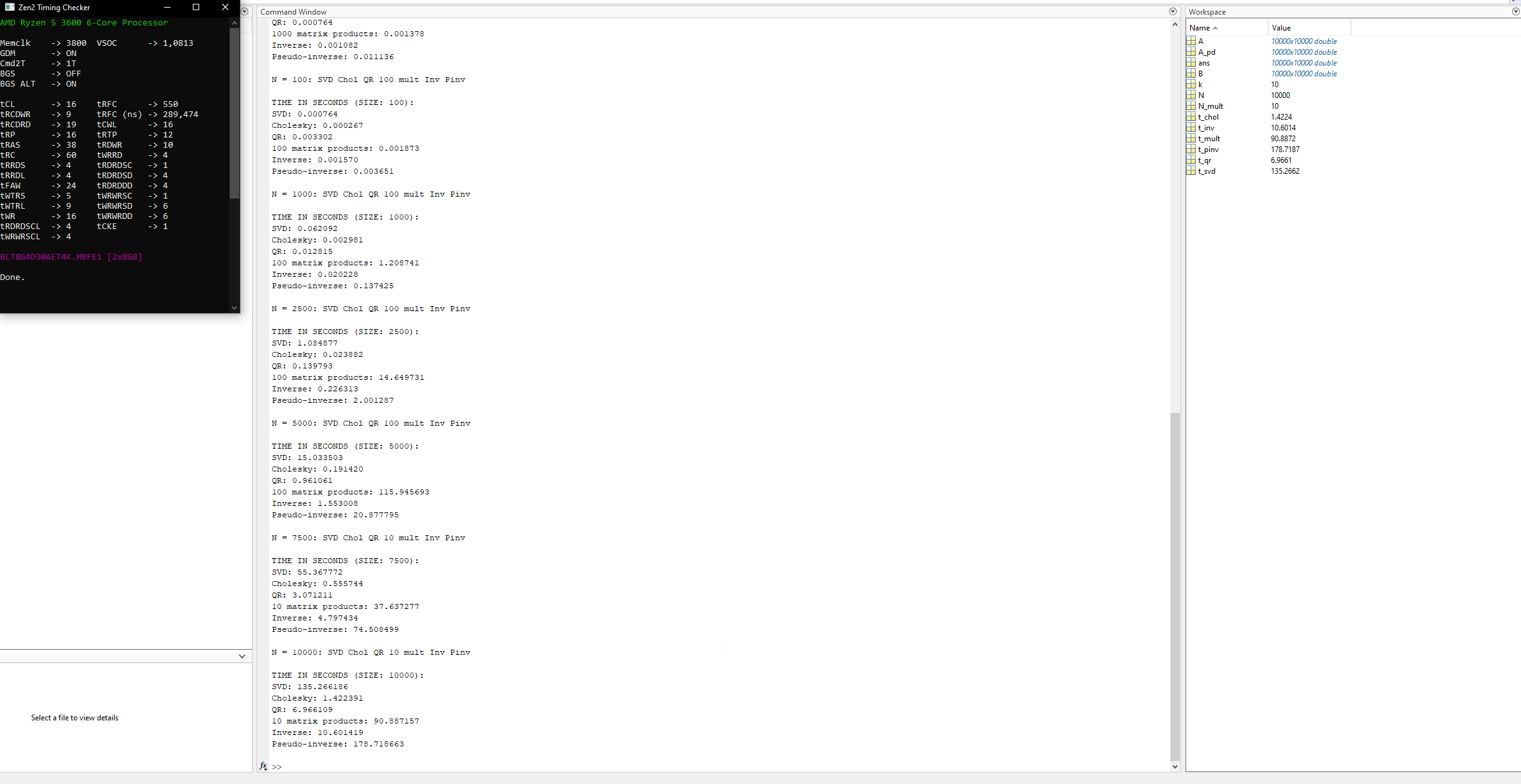
N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.002686
Cholesky: 0.000313
QR: 0.000764
1000 matrix products: 0.001378
Inverse: 0.001082
Pseudo-inverse: 0.011136

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.000764
Cholesky: 0.000267
QR: 0.003302
100 matrix products: 0.001873
Inverse: 0.001570
Pseudo-inverse: 0.003651

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.062092
Cholesky: 0.002981
QR: 0.012815
100 matrix products: 1.208741
Inverse: 0.020228
Pseudo-inverse: 0.137425

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 1.084877
Cholesky: 0.023882
QR: 0.139793
100 matrix products: 14.649731
Inverse: 0.226313
Pseudo-inverse: 2.001287

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 15.033503
Cholesky: 0.191420
QR: 0.961061
100 matrix products: 115.945693
Inverse: 1.553008
Pseudo-inverse: 20.877795

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 55.367772
Cholesky: 0.555744
QR: 3.071211
10 matrix products: 37.637277
Inverse: 4.797434
Pseudo-inverse: 74.508499

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 135.266186
Cholesky: 1.422391
QR: 6.966109
10 matrix products: 90.887157
Inverse: 10.601419
Pseudo-inverse: 178.718663

Scientist · 30. Dezember 2019

Keine Ahnung, ob noch interesse besteht, vielen Dank jedenfalls fuer den Fix

CPU: R5 1600
RAM: 16 GB (15-17-17-35@2933; CMK16GX4M2B3000C15)
MB: PRIME X370-PRO
Matlab: 2018b, bei Interesse kann ich im Januar aktualisieren.

N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.019563
Cholesky: 0.001852
QR: 0.001470
1000 matrix products: 0.002039
Inverse: 0.000469
Pseudo-inverse: 0.013180

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.001654
Cholesky: 0.000441
QR: 0.001144
100 matrix products: 0.016268
Inverse: 0.001040
Pseudo-inverse: 0.007075

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.160034
Cholesky: 0.011479
QR: 0.037925
100 matrix products: 6.165019
Inverse: 0.106432
Pseudo-inverse: 0.521690

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 3.085689
Cholesky: 0.149931
QR: 0.555291
100 matrix products: 74.762129
Inverse: 0.859907
Pseudo-inverse: 6.058650

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 24.515112
Cholesky: 0.994880
QR: 4.119311
100 matrix products: 552.681337
Inverse: 6.452710
Pseudo-inverse: 52.621012

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 92.770346
Cholesky: 3.158427
QR: 12.945868
10 matrix products: 183.994268
Inverse: 29.571296
Pseudo-inverse: 173.814415

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 202.130661
Cholesky: 7.954050
QR: 32.092163
10 matrix products: 448.642413
Inverse: 55.229863
Pseudo-inverse: 398.063089

N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.000174
Cholesky: 0.002305
QR: 0.002142
1000 matrix products: 0.001794
Inverse: 0.002826
Pseudo-inverse: 0.001732

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.005271
Cholesky: 0.000221
QR: 0.000452
100 matrix products: 0.016258
Inverse: 0.006603
Pseudo-inverse: 0.006415

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.115285
Cholesky: 0.004712
QR: 0.023297
100 matrix products: 3.375838
Inverse: 0.034084
Pseudo-inverse: 0.274654

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 2.609938
Cholesky: 0.067855
QR: 0.272475
100 matrix products: 33.553482
Inverse: 0.445010
Pseudo-inverse: 4.659665

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 24.183052
Cholesky: 0.451299
QR: 1.984860
100 matrix products: 276.532223
Inverse: 3.765842
Pseudo-inverse: 37.577808

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 78.722401
Cholesky: 1.226720
QR: 5.379061
10 matrix products: 79.249658
Inverse: 9.921155
Pseudo-inverse: 115.508299

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 189.288840
Cholesky: 3.800688
QR: 12.092002
10 matrix products: 184.282071
Inverse: 22.909531
Pseudo-inverse: 277.837739

N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.055572
Cholesky: 0.002885
QR: 0.002579
1000 matrix products: 0.001545
Inverse: 0.001889
Pseudo-inverse: 0.022328

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.001384
Cholesky: 0.000313
QR: 0.005710
100 matrix products: 0.014901
Inverse: 0.002011
Pseudo-inverse: 0.005402

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.165457
Cholesky: 0.012327
QR: 0.045064
100 matrix products: 5.095807
Inverse: 0.061331
Pseudo-inverse: 0.402559

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 2.915221
Cholesky: 0.127452
QR: 0.544514
100 matrix products: 64.185654
Inverse: 0.940771
Pseudo-inverse: 5.818031

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 24.373171
Cholesky: 0.858137
QR: 3.528556
100 matrix products: 507.325778
Inverse: 7.133361
Pseudo-inverse: 50.391461

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 92.046263
Cholesky: 2.869337
QR: 11.917141
10 matrix products: 171.126426
Inverse: 25.073256
Pseudo-inverse: 162.883930

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 216.912417
Cholesky: 7.036692
QR: 29.788876
10 matrix products: 408.942708
Inverse: 60.076411
Pseudo-inverse: 393.171555

N = 10: SVD Chol QR 1000 mult Inv Pinv

TIME IN SECONDS (SIZE: 10):
SVD: 0.000356
Cholesky: 0.000308
QR: 0.000289
1000 matrix products: 0.001220
Inverse: 0.000264
Pseudo-inverse: 0.000992

N = 100: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 100):
SVD: 0.000908
Cholesky: 0.000162
QR: 0.000297
100 matrix products: 0.004667
Inverse: 0.000463
Pseudo-inverse: 0.003742

N = 1000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 1000):
SVD: 0.092902
Cholesky: 0.004666
QR: 0.022194
100 matrix products: 2.769275
Inverse: 0.036099
Pseudo-inverse: 0.238687

N = 2500: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 2500):
SVD: 2.650536
Cholesky: 0.058471
QR: 0.265890
100 matrix products: 27.237607
Inverse: 0.378433
Pseudo-inverse: 3.838587

N = 5000: SVD Chol QR 100 mult Inv Pinv

TIME IN SECONDS (SIZE: 5000):
SVD: 21.846662
Cholesky: 0.338517
QR: 1.519652
100 matrix products: 242.623653
Inverse: 2.408578
Pseudo-inverse: 34.073707

N = 7500: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 7500):
SVD: 76.480659
Cholesky: 1.162886
QR: 5.119944
10 matrix products: 82.529187
Inverse: 9.191650
Pseudo-inverse: 110.576443

N = 10000: SVD Chol QR 10 mult Inv Pinv

TIME IN SECONDS (SIZE: 10000):
SVD: 177.924832
Cholesky: 2.599833
QR: 11.474268
10 matrix products: 169.418521
Inverse: 19.189608
Pseudo-inverse: 263.785715

Ned Flanders · 30. Dezember 2019

Merci! Ist interessant neben dem 2600x.

Und nichts zu danken. Vergiss nicht ne Supportanfrage Anfrage an mathworks zu schicken!

Je mehr Anfragen die bekommen, desto eher gibt's ne offizielle Lösung

Ned Flanders · 3. April 2020

Ich hab das Matlab Benchmark Script nochmal etwas überarbeitet. Es enthält jetzt zusätzlich noch eine Eigen Faktorisierung und ich hab die Matrix Größen mal auf etwas handhabbarere Größen gestutzt. Dauert jetzt nicht mehr 15min bis er durch ist.

for N=[48, 128, 1024, 2048, 4096]
if N<100
N_mult = 1000;
elseif N<5001
N_mult = 100;
else
N_mult = 10;
end
fprintf('N = %d: ', N);

rng(1);
A = rand(N);
B = rand(N);
A_pd = A*A';

tic;
svd(A);
t_svd = toc;
fprintf('SVD ');

tic;
eig(A);
t_eig = toc;
fprintf('Eig ');

tic;
chol(A_pd);
t_chol = toc;
fprintf('Chol ');

tic;
qr(A);
t_qr = toc;
fprintf('QR ');

tic;
for k=1:N_mult
A*B;
end
t_mult = toc;
fprintf('%d mult ', N_mult);

tic;
inv(A);
t_inv = toc;
fprintf('Inv ');

tic;
pinv(A);
t_pinv = toc;
fprintf('Pinv\n\n');

fprintf('TIME IN SECONDS (SIZE: %d):\n', N);
fprintf('SVD: %f\n', t_svd);
fprintf('Eigen: %f\n', t_eig);
fprintf('Cholesky: %f\n', t_chol);
fprintf('QR: %f\n', t_qr);
fprintf('%d matrix products: %f\n', N_mult, t_mult);
fprintf('Inverse: %f\n', t_inv);
fprintf('Pseudo-inverse: %f\n\n', t_pinv);
end

hdwfid42 · 28. Mai 2020

Same issue with fea software ANSYS Mechanical.
Small ANSYS Mechanical linear-static fea model with frictional contacts - 3 mio DOF - needs 24 GB in-core memory
Running on 8 cores with Sparse Solver and Distributed Memory Parallel (DMP).

MKL_Debug => set MKL_DEBUG_CPU_TYPE=5

Elapsed Time [sec]:
Ryzen 9 3900 vs. Ryzen 9 3900 (with MKL_Debug) vs. Xeon Gold 6136:
1259 vs. 702 vs. 676 - ANSYS 17.2 (AVX2)
1167 vs. 677 vs. 526 - ANSYS 19.2 (AVX-512)
1252 vs. 664 vs. 530 - ANSYS 2020 R1 (AVX-512)

Using the MKL-Tweak shows a speed-up of approx. 2 for the Ryzen 9 3900.

Using only AVX2 (ANSYS 17.2) the Xeon Gold and the Ryzen have approx. same speed.
With AVX-512 (ANSYS 19.2 and newer) the Xeon Gold is getting a bit faster (+22 %).

Cooling Fan Speed of the Ryzen 9 3900 is set to Max and the CPU works at 3.8 - 4.0 GHz while running ANSYS jobs on 8 cores. Xeon Gold 6136 is running here at 3.5 to 3.6 GHz.

When CPUs are using AVX2/AVX-512 the turbo frequency is a bit lower to avoid overheating

No Hyperthreading is used.
Windows 10

Denniss · 7. Juni 2020

Kann das bitte mal jemand mit MKL 2020 Update 1 prüfen ob der AMD-Workaround noch funktioniert?
Den Kommentaren nach hat Intel den Debug Mode deaktiviert der für den Workaround nötig ist.
https://old.reddit.com/r/matlab/com...matlab_to_use_a_fast_codepath_on_amd/fm2j83e/

Iscaran · 7. Juni 2020

OMG...Intel at its best...

Denniss · 7. Juni 2020

Wenn's so wäre dann wär's so ein typischer Dick Move von Intel. Aber warten wir erstmal auf Rückmeldungen.

Ned Flanders · 7. Juni 2020

Ist korrekt. Der Debug Mode wurde in U1 entfernt. Die letzte Version, die sich im Debug Mode betreiben lässt ist MKL 2020 Release Version.

Sollte auch dem Letzten die Augen bezüglich dem Sinn der Vendor String Abfrage öffnen.

Iscaran · 16. Juni 2020

Kann man denn MatLab mitteilen bzw. zwingen z.B. OpenBLAS zu verwenden ?
Da gabs ja kürzlich auch erst wieder ein deutliches Update:
https://www.phoronix.com/scan.php?page=news_item&px=OpenBLAS-0.3.10-Released

Ned Flanders · 16. Juni 2020

@Iscaran

Kann man, ich habs bislang nicht selbst getestet.

Hier der Link wie es geht.

XcIOqE · 11. Juli 2020

Ich habe demnächst vor meine Workstation zu upgraden (von 5820K, X99) und stehe vor der Wahl: AMD oder Intel. Eigentlich tendiere ich zu AMD und wollte demnächst dann auf B550 + 4900X upgraden (sollte ja Ende des Jahres kommen) oder aber sofern möglich auf 3945WX (12C/24T), 3955WX (16C/32T) (https://www.computerbase.de/2020-07/amd-ryzen-threadripper-pro-3995wx-trx80/)

Nun ist die jüngste Entwicklung bezüglich MKL ja nicht so erfreulich, weshalb Intel in Form eines 10900X oder X299 wieder im Spiel ist.

Der PC wird hauptsächlich zum Programmieren in Python, insbesondere im Bereich Machine Learning mit einschlägigen Bibliotheken wie Scikit-learn, numpy, pytorch und tensorflow genutzt. Dementsprechend ist eine hohe Multi-Core-Leistung wichtig, vereinzelt kommt es aber auch zu Single-Core Anwendungen, weshalb auch hier eine gewisse Leistung abrufbar sein sollte.

Verarbeitet werden tabellarische Daten im näheren Zeitreihen über längere Zeiträume und in größerer Anzahl. Auf Basis dieser Daten werden neuronale Netzwerke trainiert. Hyperparametersuchen werden auch gemacht, welche sich aber für gewöhnlich gut parallelisieren lassen.

Könnt ihr mir vor dem Hintergrund dieses Anwendungsszenarios einen Tipp geben?

Ned Flanders · 11. Juli 2020

Unter Linux nehm ich an?

XcIOqE · 11. Juli 2020

Ned Flanders schrieb:
Unter Linux nehm ich an?

Richtig, Ubuntu 18.04 um genau zu sein.

Wichtig zu erwähnen ist noch das ich PyCharm als IDE nutze und mich eher weniger mit Bugfixes seitens der rudimentären Software beschäftigen möchte. Also sollte das Ganze so einfach wie möglich umzusetzen sein.. Eine Umbebungsvariable zu setzen nehme ich gern in Kauf aber bei jedem Update darum bangen zu müssen ob es mir alles zerschießt möchte ich nicht.

Ned Flanders · 11. Juli 2020

Die aktuelle Situation ist schnell erklärt. Wenn du darauf angewiesen bist die aktuelle Version der mkl zu verwenden (=mkl 2020.1 oder neuer) oder das willst, dann solltest Du auf alle Fälle eine Intel CPU verwenden. Wenn du selbst kompilierst oder auch packages nach mkl aussuchen kannst, dann wäre Threadripper sicherlich eine gute Option.

Bei Intel kannst du eben noch zu einer avx512 fähigen CPU greifen, das bringt in manchen Szenarien noch einen gewissen Vorteil.

XcIOqE · 11. Juli 2020

Ned Flanders schrieb:
Wenn du selbst kompilierst oder auch packages nach mkl aussuchen kannst, dann wäre Threadripper sicherlich eine gute Option.

Soweit ich das überblicke müsste ich für jedes für mich relevante Paket, welches mkl nutzt, "build from source" anwenden? Davon habe ich leider nicht wirklich Ahnung.

Ned Flanders schrieb:
Bei Intel kannst du eben noch zu einer avx512 fähigen CPU greifen, das bringt in manchen Szenarien noch einen gewissen Vorteil.

Ja, ich habe da die X299 Plattform im Blick. Irgendwas ab 10/9940X, oder so. Bringt der DL-Boost von Intel bei den neuen 10-XXXX was außerhalb von der Bilderkennung?

Ned Flanders · 11. Juli 2020

XcIOqE schrieb:
Bringt der DL-Boost von Intel bei den neuen 10-XXXX was außerhalb von der Bilderkennung?

Bei dem was du vorhast sehe ich da keinen Vorteil.

XcIOqE · 14. Juli 2020

Dankeschön!

Übrigens braucht mein 5820k @4.3GHz
1) 48 Sekunden für den Numpy-Bench bei Win10 + MKL
2) 44 Sekunden bei Ubuntu 18.04 + MKL
3) 53 Sekunden für Ubuntu und openBLAS

Ned Flanders · 2. September 2020

Für die, die sich dafür interessieren wie es bei dem Thema weiter geht hab ich die aktuelle Entwicklung mal hier zusammengefasst.

Außerdem haue ich jetzt hier mal mit deutlicher Verspätung die Ergebnisse unseres kleinen Benchmark Vergleichs rein. Sorry für die Verspätung und Danke nochmal an alle Teilnehmenden! Der Übersichtlichkeit halber habe ich nicht alle CPUs mit in die Figures aufgenommen. Ihr könnt so aber gut abschätzen wo ihr etwa gelegen seid, denke ich. Ich hab leider keine Zeit da einen wirklichen Review Artikel daraus zu machen auch wenns spannend wäre (und hatte das wirklich viel zu lang vor mir her geschoben). Ich denke aber die Daten sind so relativ selbsterklärend aufbereitet.

Rechts sind jeweils zwei verschiedene Matrix Größen (7500x7500) + (10k x 10k)

Figure 1: SVD

Figure 2: Cholesky

Figure 3: QR

Figure 4: Matrix Multiplication

Figure 5: Inverse

Figure 6: Pseudo Inverse

Figure 7: RAM Scaling all tests (CPU 2600x) 2667MHz CL16 (SPD) vs 3600MHz CL15 (optimized Subtimings)

Figure 8: SMT ON vs SMT OFF (2600x)

Noch eine Randbemerkung: Wenn Matlab auf einem Dual Socket System unter Windows läuft, unbedingt SMT/Hyperthreading abschalten!. Der Windows Scheduler vergeigt es komplett!

Speziellen Dank nochmal an @Jan fürs anwerfen der Threadripper und auch an Dich nochmal sorry das ich am Ende zu wenig Zeit hatte das ganze niederzuschreiben.

Denniss · 3. September 2020

Wendell von Level1techs hat jetzt auch mal ein Video gemacht:

An dieser Stelle steht ein externer Inhalt von YouTube, der den Forumbeitrag ergänzt. Er kann mit einem Klick geladen und auch wieder ausgeblendet werden.

YouTube-Embeds laden

MKL Tweak auf Ryzen Systemen verbessert die Leistung drastisch

Mr. RAM OC

Lt. Commander

Fleet Admiral

Fleet Admiral

Newbie

Admiral

Captain

Admiral

Fleet Admiral

Captain

Fleet Admiral

Newbie

Fleet Admiral

Newbie

Fleet Admiral

Newbie

Fleet Admiral

Newbie

Fleet Admiral

Admiral