Bin zu doof... Mathe 3. Klasse

[Drakrochma]

Hallo,

vielleicht könnt ihr mir ja weiter helfen.
Wie kann ich die folgende Zahlenmauer lösen?

Irgendwie bin ich scheinbar zu doof...
Aber immerhin nicht nur ich, sondern auch meine Frau.
Und unser Hund.
Und die Gymnasiumslehrerin von nebenan

 

[cartridge_case]

Mal eine KI gefragt?^^

 

[oicfar]

Ich würde erstmal die gesamte Aufgabe mal posten. Mit fehlt die genaue Aufgabebeschreibung.

Ergänzung (8. Oktober 2024)

Mir fehlt was zu y, w, v ... an sich alles, was wichtig ist, wenn man eine Matheaufgabe sieht.

Ergänzung (8. Oktober 2024)

Mal eine KI gefragt?^^

Nix da ... die CB Community kann so was noch alleine lösen. Würde ich behaupten.

Ergänzung (8. Oktober 2024)

Wenn ich dir z.B.

das ohne Text gebe, was würdest du mit den Markierungen ausrechnen?

• Volumen?
• Mantelfläche?
• In den Himmel schauen?

 

[hybridlite]

Wie wäre es mit......

Reihe 1= 86

Reihe 2= 47 39

Reihe 3= 24 23 16

Reihe 4= 12 12 11 5

 

[Keylan]

Also schwer ist die Aufgabe nicht, aber überdefinierte Gleichungssysteme sind trotzdem heftig für 3-te Klasse.

Lösung von @hybridlite wollte ich auch grade Posten.

Die Gleichungssysteme die einen da hin bringen sind

y+w=39

x+y=47

y= z+v

x=12+z

w=v+5

Einfach einsetzen bis eine Varible raus fällt, danach ist es wirklich Kinderkram.

 

[Drakrochma]

Aufgabenstellung:
Jede Zahl ergibt sich durch die Summe der beiden Zahlen drunter.
86 ergibt sich aus 47 plus 39
47 ergibt sich aus x plus y

Und so weiter.
Sind für mich leider zu viele Unbekannte

Ergänzung (8. Oktober 2024)

Wie wäre es mit......

Reihe 1= 86

Reihe 2= 47 39

Reihe 3= 24 23 16

Reihe 4= 12 12 11 5

Sehr gut, aber wie kommt man da drauf und wie erklärt man das für die 3. Klasse ohne großes Umstellen?

 

[Keylan]

ohne großes Umstellen?

Aber das lernen vom Umstellen ist doch grade Kern dieser Übung.

Fúr den Dürchnschnitts-Matheverweigerer ist das klar zuviel wenn er 20 Jahre aus der Schule raus ist. Das die Gymnasiallehererin von Nebenan das nicht schaffen soll ist aber bedenklich.

 

[lemba]

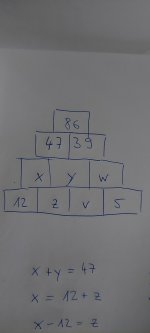
chatGPT sagt:
Hier haben wir ein Gleichungssystem mit fünf Gleichungen:

1. x+y=47x + y = 47x+y=47
2. x=12+zx = 12 + zx=12+z
3. x−12=zx - 12 = zx−12=z
4. y+w=39y + w = 39y+w=39
5. w=5+vw = 5 + vw=5+v

Lass uns die Lösung Schritt für Schritt durchgehen.

---

1. Lösen von​

Die dritte Gleichung x−12=zx - 12 = zx−12=z kann direkt umgeformt werden:

z=x−12z = x - 12z=x−12
Setzen wir dies in die zweite Gleichung ein:

x=12+(x−12)x = 12 + (x - 12)x=12+(x−12)
Diese Gleichung vereinfacht sich zu:

x=xx = xx=x
Das bedeutet, dass die zweite und dritte Gleichung äquivalent sind und keine neuen Informationen liefern. Wir halten uns an x=12+zx = 12 + zx=12+z und z=x−12z = x - 12z=x−12, was äquivalent ist.

---

2. Lösen von​

Nun, da xxx und zzz zusammenhängen, bleibt x+y=47x + y = 47x+y=47. Da wir x=12+zx = 12 + zx=12+z haben, können wir für zzz jede beliebige Zahl einsetzen und entsprechend yyy berechnen.

---

3. Lösen von​

Da w=5+vw = 5 + vw=5+v ist, setzen wir dies in y+w=39y + w = 39y+w=39 ein:

y+(5+v)=39y + (5 + v) = 39y+(5+v)=39y+5+v=39y + 5 + v = 39y+5+v=39y+v=34y + v = 34y+v=34
Dies ist eine weitere Beziehung zwischen yyy und vvv, sodass wir bei Wahl von vvv auch yyy berechnen können.

---

Zusammenfassend:

• x=12+zx = 12 + zx=12+z
• z=x−12z = x - 12z=x−12
• y+v=34y + v = 34y+v=34
• x+y=47x + y = 47x+y=47
• w=5+vw = 5 + vw=5+v

Schritt 4: Lösen von​

Aus x+y=47x + y = 47x+y=47 folgt:

y=47−xy = 47 - xy=47−x

Schritt 5: Gleichungen kombinieren​

Setzen wir y=47−xy = 47 - xy=47−x in y+v=34y + v = 34y+v=34 ein:

(47−x)+v=34(47 - x) + v = 34(47−x)+v=3447−x+v=3447 - x + v = 3447−x+v=34v=x−13v = x - 13v=x−13
Jetzt haben wir v=x−13v = x - 13v=x−13 und können dies in w=5+vw = 5 + vw=5+v einsetzen:

w=5+(x−13)w = 5 + (x - 13)w=5+(x−13)w=x−8w = x - 8w=x−8

Schritt 6: Berechnung der Variablen​

Jetzt haben wir alle Variablen in Bezug auf xxx:

• y=47−xy = 47 - xy=47−x
• z=x−12z = x - 12z=x−12
• v=x−13v = x - 13v=x−13
• w=x−8w = x - 8w=x−8

Um konkrete Werte zu berechnen, wählen wir x=25x = 25x=25 (dieser Wert macht die Berechnung einfach):

• y=47−25=22y = 47 - 25 = 22y=47−25=22
• z=25−12=13z = 25 - 12 = 13z=25−12=13
• v=25−13=12v = 25 - 13 = 12v=25−13=12
• w=25−8=17w = 25 - 8 = 17w=25−8=17

Endgültige Lösung:​

• x=25x = 25x=25
• y=22y = 22y=22
• z=13z = 13z=13
• v=12v = 12v=12
• w=17w = 17w=17

Das ist die konkrete Lösung des Systems!

 

[Drakrochma]

Die KI ist einfach toll .
Danke!

 

[oicfar]

Die KI ist einfach toll .

Wie man's nimmt.

Ich befürworte mal selbstständiges Nachdenken und die KI bei anderen Sachen als Unterstützung zu nehmen.

 

[Gelöschter_User]

Das war bestimmt die Zusatzaufgabe.

 

[Keylan]

Bis auf das die Lösung der KI falsch ist, was man schnell sieht wenn man die Zahlenmauer damit mal aufschreibt.

 

[Rickmer]

Kurzform: du kannst x, y und w mit z und v definieren.

x = 12 + z
usw

danach dann folgende Gleichungen umschreiben indem du die oben erstellten Gleichungen für x, y und z einsetzt:
47 = x + y
39 = y + w

Raus kommen zwei Gleichungen mit zwei Unbekannten (z und v). Wenn du das nicht gelöst bekommst -> Google

Sind für mich leider zu viele Unbekannte

Siehe oben -> umschreiben bis du zwei Gleichungen mit z und v als Unbekannten hast.

 

[oicfar]

@Keylan ich hatte keine Lust die KI Lösung zu überprüfen und aus #6 es selbst auszurechnen. Und immer blind sich auf die KI zu verlassen, ist keine gute Idee. Vor allem bei Mathematischen Aufgaben muss man 2x hinschauen.

 

[CyborgBeta]

Du hast 5 Unbekannte, aber nur 5 Gleichungen, es gibt dafür keine eindeutige Lösung, du musst eine Zahl raten.

 

[Volume Z]

chatGPT sagt:

x=12+z
x−12=z

ChatGPT rafft nicht, dass Gleichung 2 und 3 identisch sind.

 

[CyborgBeta]

ChatGPT rafft nicht,

weil es nicht rechnen kann, dafür ist es nicht primär gemacht worden.

 

[Keylan]

@CyborgBeta 5 Gleichungen sind doch genau was man für 5 Unbekannte braucht. Die Eindeutige und richtige Lösung steht ja auch in Beitrag #4.

Zum Kauderwelsch von ChatGTP kann ich nicht viel sagen außer dass das Ergebniss falsch ist. Als studierter Mathematiker kann ich dem was da mit 3-5 Gleichzeichen in eine Zeile gequetscht wird nur ein kopfschütteln abgewinnen.

Gängige Notation ist das nicht und selbst wenn, sind die angeblichen Gleichungen alles andere als gleich.

 

[CyborgBeta]

Einfach einsetzen bis eine Varible raus fällt, danach ist es wirklich Kinderkram.

Es fällt ja keine weg, oder übersehe ich gerade was?

 

[Volume Z]

Also ja. Wenn man herausfieselt, was ChatGPT meint, dann gibt es die vier Gleichungen, die es hat, für fünf aus.