World of Tanks [World of Tanks] Statistikdiskussionsthread

[Technocrat]

Warum sollte ein eigentlich guter Spieler mit einigen Panzern schlecht sein? Und warum sollte er sich nicht anstrengen und wieso zeigt er nicht, "wie gut er wirklich ist"?

Ich will Dir zeigen, das a) nur junge Männer noch beweisen müssen wie "gut" sie sind, b) das Statistiken gar nichts beweisen und c), das Leute, die sich bei Spielen anstrengen den Sinn eines SPIELES nicht verstanden haben. Frag Dich mal selber: warum muß man immer raushängen lassen, was man kann?

 

[cob]

@Wechhe
Weil einige Panzer einfach Schrott sind

Hier als Vergleich Tier 5 Schrott mit dem Namen Churchill 1 und VK DB. Beide sind nicht meine Lieblinge, aber der VK ist(war^^) zumindest schnell und lässt sich hier und da sinnvoll einsetzen.

Ich hab die beiden zu 100% solo und alle beiden selbst gezockt, innerhalb von ~2 Monaten, also ca. der gleiche "Skill-lvl"

Churchill 1 hat noch wenige Kämpfe, aber dem fehlt noch 5k bis zum nächsten Tank, da wird er sofort verkauft! (VK DB ist schon weg, was für eine Freude!)

Der WoT-News Entwickler sagt ja auch, dass das Tier nur auf Win-Chance einen Einfluss hat und man in jedem Tier ~2.8k EF erreichen kann, man muss nur die OP Panzer spielen

 

[EAV]

Ich würde Gewinnwahrscheinlichkeit und Siegesrate sowieso trennen. Ein guter Spieler mag eine hohe Gewinnwahrscheinlichkeit haben, nicht aber unbedingt eine hohe Siegesrate.

Ich werfe einen Würfel 50 Mal in Folge, wobei ich kein einziges Mal die Augenzahl 6 erhalte. Deshalb ist die Wahrscheinlichkeit für das Erscheinen der Augenzahl 6 beim 51. Wurf nicht größer, sie bleibt weiterhin bei 1/6 (16,67%). Dennoch hatte ich bei 50 Würfen eine relative Häufigkeit der Augenzahl 6 von 0 (0%).
Die relative Häufigkeit der Augenzahl 6 wird sich erst bei unendlich Versuchen dem Wert der Wahrscheinlichkeit für das Auftreten der Augenzahl 6 angleichen. Vorher nähert sie sich natürlich, aber ihren "finalen Wert" erreicht sie erst bei unendlich Würfelwürfen.

Ich spiele als guter Spieler mit einer Gewinnwahrscheinlichkeit von sagen wir mal 0,7 (70%) 50 Spiele und gewinne davon kein einziges. Beim 51. Spiel bleibt meine Gewinnwahrscheinlichkeit trotzdem bei 0,7 (70%) und wird nicht höher. Dennoch hatte ich bei 50 Spielen eine relative Häufigkeit der Siege (= Siegesrate) von 0 (0%).
Die Siegesrate wird sich erst bei unendlich Spielen der Gewinnwahrscheinlichkeit angleichen. Vorher nähert sie sich natürlich, aber ihren "finalen Wert" erreicht sie erst bei unendlich Spielen.

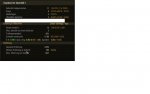
Das heißt ein guter Spieler wird nach mehreren tausend Spielen eine Siegesrate haben, die nahe seiner Gewinnwahrscheinlichkeit liegt (wobei "nahe" auch schon wieder ein dehnbarer Begriff ist):

Dieses berühmte Gesetz der Großen Zahl besagt, daß bei vielen unabhängigen Wiederholungen eines Zufallsexperiments, sei es Münzwurf, Würfeln, Lotto, Kartenspielen oder was auch immer, die relative Häufigkeit und die Wahrscheinlichkeit eines Ereignisses immer näher zusammenrücken müssen.

Quelle: Krämer, Walter: Denkste!; München; Piper Verlag GmbH; 2008, S.36

Allerdings müssen beide Werte auch nach tausenden von Spielen nicht unbedingt gleich sein. Siehe dazu z.B. auch das Würfelexperiment von Walter Krämer, das er in o.g. Buch beschreibt. Da wirft er einen Würfel 6000 Mal und erhält die Augenzahl 6 980 Mal, was einer relativen Häufigkeit von 0,1633 (16,33%) entspricht. Die Wahrscheinlichkeit für dieses Ereignis ist aber wie oben erwähnt bei 0,1667 (16,67%).


Ich hoffe, es ist einigermaßen verständlich wie ich das meine...

 

[Wechhe]

und c), das Leute, die sich bei Spielen anstrengen den Sinn eines SPIELES nicht verstanden haben.

Ernsthaft? Das ist erstens jedem selbst überlassen, was er für spaßig hält und zweitens halte ich diese These für sehr wackelig. Wenn ich ein Computerspiel im Multiplayer spiele, bei dem ich mit anderen Spielern messe, dann versuche ich automatisch gut zu sein indem ich das Spiel zu verstehen versuche, die Möglichkeiten lerne und eben versuche, zu gewinnen, bzw das Ziel des Spiels möglichst gut umzusetzen.
Das klingt so, als ob du das Spiel nur so "daddelst" und in der Gegend herumfährst, dir die Landschaft anguckst. Und wer das nicht tut, sondern versucht, gut zu sein und sich dabei anstrengt, hat den Sinn eines Spiels nicht verstanden?

Ne Techno - das ist deine Meinung - aber nicht meine. Und ich bezweifle, dass ich da alleine da stehe.

Ich will Dir zeigen, das a) nur junge Männer noch beweisen müssen wie "gut" sie sind,

Du hast du doch angefangen, vermeindlich schlechte Leute in Schutz zu nehmen und zu sagen, dass sie eigentlich besser sein können, es aber nicht sein wollen.

@EAV

Die Rechnung mit der Gewinnwahrscheinlichkeit und die Siegesrate hängen aber nicht nur vom Skill des Spielers ab. Von daher ist deine Ausführung so nicht richtig.

 

[Fetter Fettsack]

Nein. Wenn der nur Stockpanzer spielt oder nur Panzer, auf denen er nicht gut ist oder fast nur für Fun rumgurkt dan zeigt die Statistik NICHT, wie gut der Spieler tatsächlich ist, wenn er sich ins Zeug legt. Umgekehrt geht das übrigens nicht: ein tatsächlich schlechter Spiel kann nicht plötzlich gut sein. Aber wie willst Du die nur aufgrund der Statistik unterscheiden?

Ein Spieler ist so gut wie er auf dem Felde performt. Wenn einer andauernd schlecht spielt, kann er nicht plötzlich gut werden, weil ihm dazu einfach die Erfahrung fehlt. Hat er diese aber, wird er nicht schlecht spielen, weil er dann nämlich keine Lust hat nur einzustecken ohne auszuteilen ( der selige Jesus Christus vielleicht ausgenommen).

 

[Jackofalltrades]

Nein. Wenn der nur Stockpanzer spielt oder nur Panzer, auf denen er nicht gut ist oder fast nur für Fun rumgurkt dan zeigt die Statistik NICHT, wie gut der Spieler tatsächlich ist, wenn er sich ins Zeug legt. Umgekehrt geht das übrigens nicht: ein tatsächlich schlechter Spiel kann nicht plötzlich gut sein. Aber wie willst Du die nur aufgrund der Statistik unterscheiden?

Ich will auch nicht wissen wie gut er TATSÄCHLICH wäre sondern wie gut er mit dem aktuellen Panzer war und aufgrund der hohen Spielzahl auch ist und das sagt die Statistik nach einer derartigen Spielzahl aus. Nur wenn er plötzlich einen "anderen" Panzer wählt, habe ich keine Aussagekraft mehr.
Seine Motivation kann ich anhand der Statistik natürlich nicht ablesen, natürlich ebenso wenig wie seine Augenfarbe -)

Ergänzung (14. Mai 2013)

@EAV
Die Rechnung mit der Gewinnwahrscheinlichkeit und die Siegesrate hängen aber nicht nur vom Skill des Spielers ab. Von daher ist deine Ausführung so nicht richtig.

Doch das passt. Jedes Battle ist ein unabhängiges Ereignis. Der Ausgang jeden Ereignisses hängt bei WOT schon stark vom Zufall ab.
EAV hat schon vollkommen Recht.

@EAV Hast Du gegoogelt oder Krämer wirklich gelesen?

 

[Tiu]

Ein Spieler ist so gut wie er auf dem Felde performt.

Zu allgemein die Aussage mMn.
Du kannst gewinnen "weil" Du geparkt hast und Du kannst gewinnen "weil" Du nach vorne gerannt bist.
Du kannst aber auch genau aus diesen Gründen verlieren. Es ist (zumindest bei Standardgefechten) wesentlicher wie das Team als ganzes performt als die Leistung der/des einzelnen.

 

[Fetter Fettsack]

Ich bezog mich auf den Unterschied zwischen Grundlagen beachten und Grundlagen nicht beachten (also wann sollte ich mit meinem Panzer wo sein, wie verhalte mich richtig in einem Dogfight, wann sollte man schießen, wann eher nicht, etc. ). Wenn ich die ganze Zeit diese Dinge nicht beachte, dann kann ich nicht plötzlich auf einem ordentlichen Niveau aufspielen. = schlechtere Overall-performamce.

 

[Wechhe]

Ich formuliere das um:

Die Gewinnwahrscheinlichkeit eines guten Spielers wird sich in den allermeisten Fällen nicht so stark unterscheiden, dass das eine signifikante Rolle spielt. Nur bei ganz wenigen Ausnahmen - die von mir erwähnten sauguten Spieler (siehe Diskussion mit jackofalltrades ). Das liegt daran, dass andere Faktoren einen größeren Einfluss haben. Deswegen halte ich eine Gewinnwahrscheinlichkeit von 0,7 für sehr hoch, die nur in absoluten Einzelfällen erreicht wird und sich dann auch nach entsprechender, hinreichend großer Menge an Spielen an der Siegrate bemerkbar macht.

Das sind aber alles von uns statistisch nicht nachweisbare Thesen, weil uns der entsprechende Datensatz fehlt. Es ist einfach nur meine Einschätzung.

 

[Slobad]

Wahrscheinlich kann man sich über das Thema hier noch ewig auslassen. Aber ein WoT Match wird von so vielen Faktoren beeinflusst, dass eine gute Gewinnvorhersage immer schwierig wird (jaja gibt Einzelfälle, aber wie schon erwähnt wurde, die haben nix mit Statistik zu tun.)

Was ich zum Beispiel am Noobmeter sehr cool finde, dass es nicht nur die Gesamtwerte zeigt, sondern auch die der letzten ~1k Spiele und der letzten 7 Tage. Dann kann man nämlich sehen ob sich ein Spieler verbessert oder verschlechtert. Mit diesen Werten kann man viel mehr über den "Skill" aussagen als wenn man einen Mittelwert über alle Spiele betrachtet.

 

[EAV]

@EAV Hast Du gegoogelt oder Krämer wirklich gelesen?

Selbstverständlich habe ich ihn gelesen. Ich interessiere mich für Wahrscheinlichkeitsrechnung und Mathematik im allgemeinen.

Die Gewinnwahrscheinlichkeit eines guten Spielers wird sich in den allermeisten Fällen nicht so stark unterscheiden, dass das eine signifikante Rolle spielt. Nur bei ganz wenigen Ausnahmen - die von mir erwähnten sauguten Spieler (siehe Diskussion mit jackofalltrades ).

Nicht stark unterscheiden von was?

Das liegt daran, dass andere Faktoren einen größeren Einfluss haben.

Welche Faktoren? Skill ist der einzige Faktor, der die theoretische Gewinnwahrscheinlichkeit der Spieler unterscheidet. Jeder Spieler, absolut jeder, hat Zugang zu den gleichen Mitteln: Die gleichen Panzer, die gleiche Ausrüstung, die gleichen Module, die gleiche Munition, die gleichen Karten usw.
Auf unendlich Spiele gesehen (davon gehen wir ja bei der Gewinnwahrscheinlichkeit aus - im Gegensatz zur Siegesrate) hat auch der MM keinen Einfluss mehr. Absolut alle Konditionen sind gleich - nur eben der Skill nicht.

Deswegen halte ich eine Gewinnwahrscheinlichkeit von 0,7 für sehr hoch, die nur in absoluten Einzelfällen erreicht wird und sich dann auch nach entsprechender, hinreichend großer Menge an Spielen an der Siegrate bemerkbar macht.

Die 0,7 war ein fiktiver Wert, dafür kannst du jeden anderen beliebigen Wert einsetzen, an dem Gedankengang ändert sich dadurch nichts.
Dass sie sich erst nach hinreichend großer Anzahl an Gefechten bemerkbar macht, habe ich ja so auch gesagt.

Das sind aber alles von uns statistisch nicht nachweisbare Thesen, weil uns der entsprechende Datensatz fehlt. Es ist einfach nur meine Einschätzung.

Doch, es ist nachweisbar, auch ohne Datensätze. Das Stichwort: Logisches/mathematisches Denken. Von mir aus kannst du das Würfelexperiment von Walter Krämer nachmachen, dann hast du einen Beweis, den man ohne Weiteres auf WoT übertragen kann.


PS: Auch wenn es teilweise recht harsch klingen mag, soll es kein Angriff sein.

 

[Jackofalltrades]

Welche Faktoren? Skill ist der einzige Faktor, der die theoretische Gewinnwahrscheinlichkeit der Spieler unterscheidet. Jeder Spieler, absolut jeder, hat Zugang zu den gleichen Mitteln: Die gleichen Panzer, die gleiche Ausrüstung, die gleichen Module, die gleiche Munition, die gleichen Karten usw.
Auf unendlich Spiele gesehen (davon gehen wir ja bei der Gewinnwahrscheinlichkeit aus - im Gegensatz zur Siegesrate) hat auch der MM keinen Einfluss mehr. Absolut alle Konditionen sind gleich - nur eben der Skill nicht.

Man muss Siegesrate und Gewinnwahrscheinlichkeit trennen. Beides sind grundverschiedene Begriffe.

Nur der Vollständigkeit halber. In beiden Fällen kommt jedoch die Hardwareausstattung und Internetanbindung hinzu, die die Gewinnwahrscheinlichkeit beeinflussen. Hardwareausstattung ist etwas theoretisch, will sagen, daß ich mir nicht sicher bin ob dies überhaupt bei WOT relevant ist, es also noch Rechner gibt, die den Spieler "ausbremsen" könnten. Die Auswirkung der Internetanbindung braucht man nicht erklären, denke ich. Beide Faktoren sind hier aber nicht wirklich wichtig(Für die Deutung statistischer Daten durchaus).

Das unabhängige Ereignis Battle hat 3 mögliche Ergebnisse. Sieg, Niederlage oder Unentschieden. Leider macht das Unentschieden die Analogie ein wenig kaputt, da wir nicht 33% Wahrscheinlichkeit pro Ergebnis haben. Wir ignorieren das einfach mal.
Jeder Spieler hat grundsätzlich eine Gewinnwahrscheinlichkeit von 48,9%(nix errechnet-bin faul. Der Wert für Unentschieden ist bereits ein statistischer Wert, was auch vollkommen korrekt ist) und die Siegrate sollte sich diesem Wert angleichen. Abweichungen sind nach ausreichender Battlezahl durch „Skill“ entstanden. Es gibt, bis auf die beiden erwähnten“ Punkte keine anderen Einflussfaktoren. Alle Zufälle haben sich egalisiert(Es gibt im Spiel keinen Einfluss der sich nur positiv/negativ für mich oder mein Team auswirkt) – deshalb die hohe Battlezahl.

Nach einer unendlichen Anzahl an Spielen werde ich Spieler haben deren Gewinnwahrscheinlichkeit nicht mit der Siegesrate übereinstimmt. Dies liegt letztlich daran, daß die Siegrate durch Skill beeinflusst werden kann. Üblicherweise trägt man diesem Umstand durchaus Rechnung und passt für die entsprechenden Spieler die Gewinnwahrscheinlichkeit an. So hat Bayern München sicher keine 33% Gewinnchance gegen den FC . St Pauli.

 

[Bl4cke4gle]

Letztlich könnte man tatsächlich sinnvolle und gute Daten ausgeben. Man müsste nur eine Entwicklung des Spielers berücksichtigen. Selbst eine Datenauswertung basierend auf den letzten z.B. 100 Spielen wäre aussagekräftiger als der Datenwust der Vergangenheit.

Das wäre in der Tat eine super Möglichkeit. Ich würde den Wert wahrscheinlich auf 500 oder 1000 erhöhen, aber prinzipiell wäre es echt super. Vielleicht lässt XVM das ja mit den neuen Statistikwerten zu, die ab dem nächsten Update zur Verfühgung stehen sollen.

 

[LoopNBj]

Ich selber nutze zur Beurteilung eines Spielers wenn überhaupt nur Skillratings der letzten wenigen Gefechte (100-500) um eine Tendenz ableiten zu können. Genaueres wäre natürlich schön, wenn man jeden einzelnen Panzer betrachten könnte. Zumindest ist dies notwendig, wenn ein Spieler noch nicht allzu viele Gefechte hinter sich hat (z.B. ~2500-5000), denn ab 10.000 ist es mMn so, dass die anfänglichen Fehler relativ gut durch die darauf folgenden Gefechte relativ gut beglichen sind.

 

[Technocrat]

Im Ernst, Loop, ich brauche 2 min im Gefecht mit ihm, egal ob auf meiner oder der Gegenseite, und ich weiß was er taugt. Da ist keine Statistik nötig, im Gegenteil, wie ich hier schon mehrfach dargelegt habe, verschleiert eine solche nur.

 

[LoopNBj]

Ja und auch wieder nein. Dadurch, dass ich vor allem mit neuen Panzern eine schwankende Leistung habe, würde ich nicht von einem einzelnen Gefechtseindruck darauf schließen, ob er/ich wirklich schlecht ist/bin. Um es mal so zu sagen: Diese Stichprobe ist viel zu klein.
Dennoch zeigt sich bei Beschuss sofort, ob der Spieler intelligent reagiert, oder einfach nur dumm rumsteht --> vermutlich dann doch eher ein schlechterer Spieler.

 

[Wechhe]

@ Techno

Eine Statistik über alle Matches mit vielen Parametern hat also weniger Aussagekraft als eine 2-minütige Beobachtung?

Deiner Meinung nach ist ja eine Statistik nicht aussagekräftig, weil es sein kann, dass man sich nicht anstrengt (sonst hat man deiner Meinung nach SPIELEN ja nicht verstanden), weil man mit einem Stockpanzer fährt oder mit Panzern, in denen man nicht gut ist.
Das sind aber die gleichen Gründe, warum du nach 2 Minuten nicht einschätzen kannst, ob jemand gut oder schlecht ist - dieser jemand kann dir nach deinem Urteil genau das entgegen halten.

 

[Technocrat]

Eine Statistik über alle Matches mit vielen Parametern hat also weniger Aussagekraft als eine 2-minütige Beobachtung?

Aber absolut, und zwar weil sie nur die Vergangenheit wiederspieglt und prinzipbedingt NICHTS über Gegenwart oder Zukunft sagen kann. Meine Methode ist aber aussagekräftig für das aktuelle Gefecht, und nur darauf kommt es an. Wie gut der Spieler ist wenn seine kleine Schwester nicht an der Maus sitzt, ist mir egal: jetzt ist die Kleine am Steuer und darauf muß ich mich einstellen und nicht darauf, das ihr Bruder ein Starspieler ist.

 

[Wechhe]

Aber absolut, und zwar weil sie nur die Vergangenheit wiederspieglt und prinzipbedingt NICHTS über Gegenwart oder Zukunft sagen kann.

In dem Punkt widerspreche ich dir. Statistiken sind nur eine Auswertung von Daten. Und ich kann die Art der Berechnung ja meiner Fragestellung anpassen - zum Beispiel nur die letzten 3 Wochen betrachten. Aber dass du das so kategorisch ausschließt und so schwarz/weiß siehst, finde ich ziemlich krass. "prinzipbedingt NICHT" - das ist meiner Meinung nach zu pauschal.

Meine Methode ist aber aussagekräftig für das aktuelle Gefecht, und nur darauf kommt es an.

Da kann ich dir aber deine eigenen Argumente vorhalten. "Derjenige kann doch aber nur just for fun gespielt haben, ohne sich angestrengt zu haben, mit einem Panzer auf dem er nicht so gut ist, weil er soviele verschiedene Panzer spielt. In Wirklichkeit könnte er doch viel besser sein!"
Du willst aufgrund eines einzigen Gefechts (oder sogar nur 2 minuten davon) die Fähigkeiten eines Spielers abgeklärt haben? Eine grobe Einschätzung mit Fehlerwahrscheinlichkeit wäre da eher angebracht.

 

[Technocrat]

Schon. Es ist ja nur für dieses Gefecht. Und wenn der im Moment keinen Bock hat, merkt man das auch.

Und jetzt erklärst Du mir bitte noch mal ernsthaft und überzeugend, daß statistische Daten in irgendeiner Weise einen Einzelfall beschreiben können. Da wiehert jeder Versicherungssachbearbeiter...